Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T03:59:35.764Z Has data issue: false hasContentIssue false
  • English
  • Français

A Decomposition of Measures

Published online by Cambridge University Press:  20 November 2018

Norman Y. Luther
Norman Y. Luther*
Affiliation:
Washington State University, Pullman, Washington
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a set, 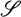a σ-ring of subsets of X, and let μ be a measure on 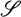. Following (1), we define μ to be semifinite if

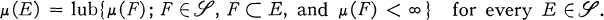
We show (Theorem 1) that every measure can be reduced to a semifinite measure for many practical purposes. In many cases, this reduction can be made even more significantly (Theorems 2 and 3). Finally, necessary and sufficient conditions that a semifinite measure be c-finite are given as a corollary to Theorem 3.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 953 - 959
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Berberian, S. K., Measure and integration (Macmillan, New York, 1965).Google Scholar
2. Halmos, P. R., Measure theory (Van Nostrand, New York, 1950).10.1007/978-1-4684-9440-2CrossRefGoogle Scholar
3. Hewitt, E. and Stromberg, K., Real and abstract analysis (Springer-Verlag, New York, 1965).Google Scholar
4. Johnson, R. A., On the Lebesgue decomposition theorem, Proc. Amer. Math. Soc. 18 (1967), 628–632.Google Scholar