Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T12:58:26.103Z Has data issue: false hasContentIssue false
  • English
  • Français

Dilations and Hahn Decompositions for Linear Maps

Published online by Cambridge University Press:  20 November 2018

D. W. Hadwin
D. W. Hadwin*
Affiliation:
University of New Hampshire, Durham, New Hampshire
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose is a C*-algebra and H is a Hilbert space. Let 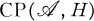denote the set of completely positive maps from into the set B(H) of (bounded linear) operators on H. This paper studies the vector space 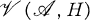spanned by 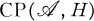, i.e., the linear maps that are finite linear combinations of completely positive maps. From another viewpoint, a map ϕ is in 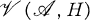precisely when it has a decomposition ϕ = (ϕ1 – ϕ2) + i(ϕ3 – ϕ4) with ϕ1, ϕ2, ϕ3, ϕ4 in CP 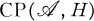; this decomposition is analogous to the Hahn decomposition for measures [8, 111.4.10] (see also Theorem 20). The analogous class of maps with “completely positive” replaced by “positive” was studied by R. I. Loebl [11] and S.-K. Tsui [17], and when is commutative, this latter class coincides withi 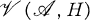, since every positive linear map on a commutative C*-algebra is completely positive [16].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 4 , 01 August 1981 , pp. 826 - 839
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Arveson, W., Subalgebras of C*-algebras, Acta Math. 123 (1969), 141–224.Google Scholar
2. Barnes, B. A., The similarity problem for representations of a B*'-algebra, Michigan Math. J. 22 (1975), 25–32.Google Scholar
3. Berberian, S. K., Notes on spectral theory, Van Nostrand, Math. Studies No. 5 (Princeton, 1966).Google Scholar
4. Berberian, S. K., Approximate proper vectors, Proc. AMS 13 (1962), 111–114.Google Scholar
5. Bunce, J. W., Representations of strongly amenable C*-algebras, PAMS 32 (1972), 241–246.Google Scholar
6. Bunce, J. W., The similarity problem for representations of C*-algebras, preprint (1980).Google Scholar
7. Christensen, E., On non self-adjoint representations of C*-algebras, preprint (1980).Google Scholar
8. Dunford, N. and Schwartz, J. T., Linear operators I, II, III (Wiley, Interscience, New York).Google Scholar
9. Hadwin, D. W. and Nordgren, E. A., Subalgebras of reflexive algebras, preprint (1980).Google Scholar
10. Kadison, R. V., On the orthogonalization of operator representations, Amer. J. Math. 77 (1955), 600–620.Google Scholar
11. Loebl, R. I., A Hahn decomposition for linear maps, Pacific J. Math. 65 (1976), 119–133.Google Scholar
12. Loebl, R. I., Contractive linear maps on C*-algebras, Michigan Math. J. 22 (1975), 361–366.Google Scholar
13. Naimark, M. A., On a representation of operator set functions, Doklady Akad Nauk SSSR (N.S.) 41 (1943), 359–361.Google Scholar
14. Sakai, S., C*-algebras and W*-algebras, Ergebn. Math. Grenzgeb. 60 (Springer, Berlin, 1971).Google Scholar
15. Sarason, D. E., On spectral sets having connected complement, Acta. Sci. Math. (Szeged) 26 (1965), 289–299.Google Scholar
16. Stinespring, W. F., Positive functions on C*-algebras, PAMS 6 (1955), 211–216.Google Scholar
17. Tsui, S.-K., Decompositions of linear maps, TAMS 230 (1977), 87–112.Google Scholar
18. Wright, S., On orthogonalization of C*''-algebras, Indiana Univ. Math. J. 27 (1978), 383–399.Google Scholar