Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hursey, R. J.
1971.
On ordered polycyclic groups.
Proceedings of the American Mathematical Society,
Vol. 28,
Issue. 2,
p.
391.
Mura, Roberta Botto
1974.
Right-Ordered Polycyclic Groups.
Canadian Mathematical Bulletin,
Vol. 17,
Issue. 2,
p.
175.
Hursey, Robert J.
1989.
On nilpotent and polycyclic groups.
Bulletin of the Australian Mathematical Society,
Vol. 40,
Issue. 1,
p.
119.

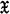 denote the class of all (fully) ordered groups satisfying the maximal condition on subgroups, and let
denote the class of all (fully) ordered groups satisfying the maximal condition on subgroups, and let 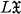 denote the class of all locally
denote the class of all locally 