Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-25T06:17:26.572Z Has data issue: false hasContentIssue false
  • English
  • Français

Zeta Functions on the Unitary Sphere

Published online by Cambridge University Press:  20 November 2018

S. Minakshisundaram
S. Minakshisundaram*
Affiliation:
Waltair, S.India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

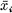In an earlier paper [5], the author defined a zeta function on the real sphere , whereas in the present paper it is proposed to define one on the unitary sphere where xi's are complex numbers and their complex conjugates. Following E. Cartan, harmonics on the unitary sphere are defined and then a zeta function formed just as in the case of a real sphere. The unitary sphere is seen to behave like an even-dimensional closed manifold, since results similar to the ones proved by the author and A. Pleijel [6] for closed manifolds (of even dimensions) are observed here also.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 4 , 1952 , pp. 26 - 30
Copyright
Copyright © Canadian Mathematical Society 1952

References

1. Bailey, W. N., Generalized hypergeometric series, Cambridge Tract No. 32 (1935).Google Scholar
2. Cartan, E., Leçons sur la géométrie projective complexe (Paris, 1931).Google Scholar
3. Cartan, E., Sur la détermination d'un systéme orthogonal complet dans un espace de Riemann symétrique clos, Rend. Cire. Mat. di Palermo, vol. 53 (1929), 217–252.Google Scholar
4. Casimir, H. B. G., Rotation of a rigid body in quantum mechanics, Leiden thesis (1931).Google Scholar
5. Minakshisundaram, S., Zeta function on the sphere, J. Ind. Math. Soc, vol. 13 (1949), 41–48.Google Scholar
6. Minakshisundaram, S. and Pleijel, A., Some properties of the eigenfunction of the Laplace operator on Riemann manifolds, Can. J. Math., vol. 1 (1949), 242–286.Google Scholar
7. Weyl, H., Harmonics on homogeneous manifolds, Annals of Math., vol. 35 (1934), 485–499.Google Scholar
8. Weyl, H., Ramification, old and new, of the eigenvalue problem, Bull. Amer. Math. Soc, vol. 56 (1950), 15–139.Google Scholar