Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-01T04:05:49.030Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute Summability Factors in a Sequence

Published online by Cambridge University Press:  20 November 2018

S. Baron
S. Baron*
Affiliation:
Department of Mathematics and Computer Science Bar Ilan University 52 100 Ramat Gan, Israel
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let α≥0 and β>— 1. The main result gives necessary and sufficient conditions for the sequence (εn) in order that the sequence (εnUn) will be absolutely summable by the Cesàro method Cβ for each sequence (Un) which is bounded or summable by the method Cα

Another theorem is proven when Cα and Cβ are replaced by triangular methods A = (ank) and B=(bnk) satisfying 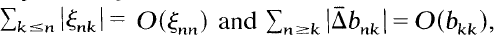, where (ξnk) = (ank)-1.

Keywords

40D1540 G 05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 1 , 01 March 1984 , pp. 16 - 30
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Abel, M., About ψ-convergence factors for complex order Cesàro's summation methods, Tartu Ülikooli Toimetised 253 (1970), 179-193 (in Russian); MR 44, #684.Google Scholar
2. Abel, M. and Tjurnpu, H., On ψ-convergence factors, Tartu Ülikooli Toimetised 206 (1967), 106-121 (in Russian); MR41 #7336.Google Scholar
3. Ahmad, Z. U. and Khan, M. R., On absolute Abel summability factors in a sequence, Indian J. Pure Appl. Math. 8 (1977), no. 11, 1402-1406.Google Scholar
4. Andersen, A. F., Studies over Cesàro's Summabilitetsmetode, Kobenhavn, 1921 (in Danish).Google Scholar
5. Baron, S., Neue Beweise der Hauptsätze für Summierbarkeitsfaktoren, Izv. Akad. Nauk Eston. SSR. Ser. Tehn. Fiz-Mat. Nauk 9 (1960), 47–68 (in Russian); Zbl 100, p. 58–9, MR 24, #A363.Google Scholar
6. Baron, S., Introduction to the Theory of Summability of Series (Second Edition, corrected and supplemented), Tallinn, "Valgus", 1977 (in Russian), MR 81j: 40007.Google Scholar
7. Baron, S., Absolute summability factors in a sequence, Tartu Ülikooli Toimetised 504 (1981), 35-47 (in Russian).Google Scholar
8. Baron, S., On a generalization of a theorem of B. Tyler, Isr. J. Math. 43 (1982), no. 2, 105-115.Google Scholar
9. Bosanquet, L. S., Note On The Bohr-Hardy Theorem, J. London Math. Soc. 17 (1942), 166-173.Google Scholar
10. Bosanquet, L. S., Note on convergence and summability factors, III, Proc. London Math. Soc. (2), 50 (1949), 482-496.Google Scholar
11. Bosanquet, L. S., On convergence and summability factors in a sequence, Mathematika 1 (1954), no. 1, 24-44.Google Scholar
12. Bosanquet, L. S. and Chow, H. C., Some remarks on convergence and summability factors, J. London Math. Soc. 32 (1957), 73-82.Google Scholar
13. Chow, H. C., Note on convergence and summability factors, J. London Math. Soc. 29 (1954), 459-476.Google Scholar
14. Espenberg, H., Summability factors in a sequence for the Euler-Knopp method, Sb. Naucn. Trudov Est. Selsk.-Hoz. Akad. 31 (1963), 73-81 (in Russian).Google Scholar
15. Hardy, G. H., Divergent Series, Oxford, Clarendon, 1949.Google Scholar
16. Peyerimhoff, A., Untersuchungen iiber absolute Summierbarkeit, Math. Z. 57 (1957), no. 3, 265-290.Google Scholar
17. Peyerimhoff, A., Summierbarkeitsfaktoren für absolut Cesàro-summierbare Reihen, Math. Z. 59 (1954), 417-424.Google Scholar
18. Peyerimhoff, A., Über Summierbarkeitsfaktoren und verwandte Fragen bei Cesàroverfahren I, Acad. Serbe Sci. Publ. Inst. Math. 8 (1955), 139-156; MR 17, 1076.Google Scholar
19. Peyerimhoff, A., Über Summierbarkeitsfaktoren und verwandte Fragen bei Cesàroverfahren II, Acad. Serbe Sci. Publ. Inst. Math. 10 (1956), 1-18; MR 18, 651.Google Scholar
20. Peyerimhoff, A., Über ein Lemma von Herm Chow, J. London Math. Soc. 32 (1957), no. 1, 33-36; MR 18, 651.Google Scholar
21. Tyler, B., Absolute convergence and summability factors in a sequence, J. London Math. Soc. 33 (1958), 341-351; MR 20 #5378.Google Scholar
22. Zeller, K., Matrixtransformationen von Folgenrä;umen, Univ. Roma. 1st. Naz. Alta Mat. Rend. Mat. e Appl. (5) 12 (1953), 340–346; MR 15, 618.Google Scholar
23. Zygmund, A., Trigonometric Series, Vol. 1, Cambridge, 1968.Google Scholar