Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jha, Pranava K.
Agnihotri, Naveen
and
Kumar, Rajesh
1997.
Long cycles and long paths in the Kronecker product of a cycle and a tree.
Discrete Applied Mathematics,
Vol. 74,
Issue. 2,
p.
101.
Král', Daniel
Maxová, Jana
Šámal, Robert
and
Podbrdský, Pavel
2005.
Hamilton cycles in strong products of graphs.
Journal of Graph Theory,
Vol. 48,
Issue. 4,
p.
299.
Flandrin, Evelyne
Li, Hao
and
Čada, Roman
2006.
Hamiltonicity and pancyclicity of generalized prisms.
Electronic Notes in Discrete Mathematics,
Vol. 24,
Issue. ,
p.
61.
Král', Daniel
and
Stacho, Ladislav
2008.
Hamiltonian threshold for strong products of graphs.
Journal of Graph Theory,
Vol. 58,
Issue. 4,
p.
314.
2011.
Handbook of Product Graphs.
p.
447.
de Wiljes, Jan-Hendrik
and
Kreh, Martin
2023.
Peg solitaire on graphs — A survey.
Asian-European Journal of Mathematics,
Vol. 16,
Issue. 04,

 denote the graph
denote the graph  (k times) where
(k times) where 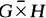 is the strong product of the two graphs
is the strong product of the two graphs  is hamiltonian.
is hamiltonian.