Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T00:40:22.238Z Has data issue: false hasContentIssue false
  • English
  • Français

Products and Cardinal Invariants of Minimal Topological Groups

Published online by Cambridge University Press:  20 November 2018

Douglass L. Grant  and
W. W. Comfort
Douglass L. Grant
Affiliation:
University College of Cape Breton, Box 5300, Sydney, Nova Scotia, Canada BIP 6L2
W. W. Comfort
Affiliation:
University College of Cape Breton, Box 5300, Sydney, Nova Scotia, Canada BIP 6L2
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is a question of Arhangel'skiĭ [1] (Problem 2) whether the identity ψ(G) = X(G) holds for every minimal Hausdorff topological group G = 〈G,u〉). (Here, as usual, ψ(G), the pseudocharacter of G, is the least cardinal number K for which there is 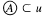such that 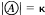and 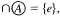and x(G), the character of G,is the least cardinality of a local base at e for (〈G,u〉.) That 〈G, u〉 is minimal means that, if v is a Hausdorff topological group topology for G and v ⊂ u, then v = u.

In this paper, we give some conditions on G sufficient to ensure a positive response to Arhangel'skiï's question, and we offer an example which responds negatively to a question on minimal groups posed some years ago (cf. [6] (p. 107) and [4] (p. 259)).

Keywords

Primary 54A2554D25Secondary 22A0554A10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 29 , Issue 1 , 01 March 1986 , pp. 44 - 49
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Arhangel'skiĭ, A. V., Cardinal invariants of topological groups, embeddings and condensation, Soviet Math. Doklady 20 (1979), pp. 783–787.Google Scholar
2. Bourbaki, N., Topologie Générale, Chapitres 3 et 4, (Actualités Scientifiques et Industrielles, No. 1143.) Hermann. Paris, France. 1980.Google Scholar
3. Brown, L. G., Topologically complete groups, Proc. Amer. Math. Soc. 35 (1972), pp. 593–600.Google Scholar
4. Comfort, W. W. and Grant, Douglass L. Cardinal invariants, pseudocompactness and minimality: some recent advances in the topological theory of topological groups, Topology Proceedings 6 (1981), pp. 227–265.Google Scholar
5. Engelking, Ryszard, General Topology, Polska Akademia Nauk, Monographie Matematyczne volume 60. Panstwowe Wydawnictwo Naukowe—Polish Scientific Publishers. Warszawa. 1977.Google Scholar
6. Grant, Douglass L., Topological groups which satisfy an open mapping theorem, Pacific J. Math. 68 (1977), pp. 411–423.Google Scholar
7. Grant, Douglass L., Arbitrary powers of the roots of unity are minimal Hausdorff topological groups. Topology Proceedings 4 (1979), pp. 103–108.Google Scholar
8. Grant, D. L. and Comfort, W. W., Infinite products and cardinal invariants of minimal topological groups (preliminary report), Notices Amer. Math. Soc. 2 (1981), pp. 540–541.[Abstract 81T-22-564].Google Scholar
9. Guran, I. I., On topological groups close to being Lindelöf, Doklady Akad. Nauk SSSR 256 (1981), pp. 1305–1307. [In Russian. English translation: Soviet Math. Doklady 23 (1981), 173-175.]Google Scholar
10. Hewitt, Edwin and Ross, Kenneth A., Abstract Harmonic Analysis, Volume I. Grundlehren der math. Wissenschaften volume 115. Springer-Verlag. Berlin-Göttingen-Heidelberg. 1963.Google Scholar
11. Husain, Taqdir, Introduction to Topological Groups, W. B. Saunders Company. Philadelphia and London. 1966.Google Scholar
12. Nagata, J., On a necessary and sufficient conditions of metrizability, J. Inst. Poly tech. Osaka City Univ. 1 (1950), pp. 93–100.Google Scholar
13. Stephenson, R. M., Minimal topological groups, Mathematische Annalen 192 (1971), pp. 193—195.Google Scholar
14. Stojanov, Luchesar N., On products of minimal and totally minimal groups, In: Proc. Eleventh Spring Conference (1982) of the Bulgarian Mathematical Society of Slunchev brjag, pp. 79-91. Bulgarian Academy of Sciences. Sophia, Bulgaria. 1982.Google Scholar
15. Sulley, L. J., A note on B- and Br-complete topological abelian groups, Proc. Cambridge Phil. Soc. 66 (1969), pp. 275–279.Google Scholar