Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T13:33:20.090Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur la borne inférieure du rang du 2-groupe de classes de certains corps multiquadratiques

Published online by Cambridge University Press:  20 November 2018

A. Mouhib
A. Mouhib*
Affiliation:
Univ. Mohammed Ben Abdellah, Faculté polydisciplinaire, Laboratoire d’Informatique, Mathématiques, Automatique et Optoélectronique, B/P 1223, Taza-Gare, Maroccourriel: mouhibali@yahoo.fr
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soient 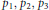${{p}_{1}},\,{{p}_{2}},\,{{p}_{3}}$ et $q$ des nombres premiers distincts tels que 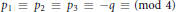${{p}_{1}}\,\equiv \,{{p}_{2}}\,\equiv \,{{p}_{3}}\,\equiv \,-q\,\equiv \,1\,(\bmod \,4)$, 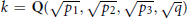$k=\mathbf{Q}(\sqrt{{{p}_{1}}},\sqrt{{{p}_{2}}},\sqrt{{{p}_{3}}},\sqrt{q})$ et 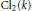$\text{C}{{\text{l}}_{2}}(k)$ le 2-groupe de classes de $k$. A. Fröhlich a démontré que 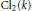$\text{C}{{\text{l}}_{2}}(k)$ n’est jamais trivial. Dans cet article, nous donnons une extension de ce résultat, en démontrant que le rang de 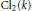$\text{C}{{\text{l}}_{2}}(k)$ est toujours supérieur ou égal à 2. Nous démontrons aussi, que la valeur 2 est optimale pour une famille infinie de corps $k$.

Abstract

Abstract

Let 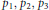${{p}_{1}},\,{{p}_{2}},\,{{p}_{3}}$ and $q$ be distinct prime numbers such that 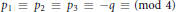${{p}_{1}}\,\equiv \,{{p}_{2}}\,\equiv \,{{p}_{3}}\,\equiv \,-q\,\equiv \,1\,(\bmod \,4)$, 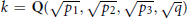$k=\mathbf{Q}(\sqrt{{{p}_{1}}},\sqrt{{{p}_{2}}},\sqrt{{{p}_{3}}},\sqrt{q})$ and 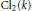$\text{C}{{\text{l}}_{2}}(k)$ the 2-class group of $k$. A. Fröhlich has shown that 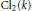$\text{C}{{\text{l}}_{2}}(k)$ can never be trivial. In this article, we give an extension of this result by proving that the rank of 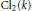$\text{C}{{\text{l}}_{2}}(k)$ is greater or equal to 2. 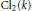Moreover, we prove that there exist infinitely many fields $k$ in which the rank of $\text{C}{{\text{l}}_{2}}(k)$ is equal to 2.

Keywords

11R2911R11class groupunitsmultiquadratic number fields
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 2 , 01 June 2011 , pp. 330 - 337
Copyright
Copyright © Canadian Mathematical Society 2011

References

Références

[A-M-1] Azizi, A. et Mouhib, A., Sur le rang du 2-groupe de classes de où m = 2 ou un premier p ≡ 1 (mod 4). Trans. Amer. Math. Soc. 353(2001), 2741–2752. doi:10.1090/S0002-9947-01-02753-2Google Scholar
[A-M-2] Azizi, A. et Mouhib, A., Capitulation des 2-classes d’idéaux de où d est un entier naturel sans facteurs carrés. Acta Arith. 109(2003), 27–73. doi:10.4064/aa109-1-2Google Scholar
[B-1] Bulant, M., On the Parity of the Class Number of the Fields . J. Number Theory 68(1998), 72–86. doi:10.1006/jnth.1997.2190Google Scholar
[B-2] Bulant, M., Class Number Parity of a Compositum of Five Quadratic Fields. Acta Math. Inform. Univ. Ostraviensis 10(2002) 25–34.Google Scholar
[B-L-S] Benjamin, E., Lemmermeyer, F. and Snyder, C., Imaginary quadratic fields with cyclic cl2 (k 1) . J. Number Theory 67(1997), 229–245. doi:10.1006/jnth.1997.2174Google Scholar
[B-S] Benjamin, E. and Snyder, C., Real quadratic number fields with 2-class group of type (2, 2) . Math. Scand. 76(1995), 161–178.Google Scholar
[F] Fröhlich, A., Central Extensions, Galois Groups, and Ideal Class Groups of Number Fields. Contemp. Math. 24, Amer. Math. Soc., Providence, 1983.Google Scholar
[H] Hasse, H., Neue Begründung und Verallgemeinerung der Theorie des Normenrestsymbols. J. Reine Angew. Math. 162(1930), 143–144.Google Scholar
[K] Kaplan, P., Sur le 2-groupe des classes d’idéaux des corps quadratiques. J. Reine Angew. Math. 283/284(1976), 313–363.Google Scholar
[Ku] Kučera, R., On the parity of the class number of a biquadratic field. J. Number Theory 52(1995), 43–52. doi:10.1006/jnth.1995.1054Google Scholar
[Kur] Kuroda, S., Uber die Dirichletschen Körper. J. Fac. Sci. Imp. Univ. Tokyo 4(1943), 382–406.Google Scholar
[M-M] Mouhib, A. et Movahhedi, A., Sur le 2-groupe de classes des corps multiquadratiques réels. J. Théor. Nombres Bordeaux 17(2005), 619–641.Google Scholar
[W] Wada, H., On the class number and the unit group of certain algebraic number fields. J. Fac. Sci. Univ. Tokyo Sect. I 13(1966), 201–209.Google Scholar