Article contents
Invariant measures for 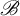 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
Published online by Cambridge University Press: 08 March 2024
Abstract
For 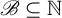 $\mathscr {B} \subseteq \mathbb {N} $, the
$\mathscr {B} \subseteq \mathbb {N} $, the 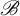 $ \mathscr {B} $-free subshift
$ \mathscr {B} $-free subshift 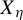 $ X_{\eta } $ is the orbit closure of the characteristic function of the set of
$ X_{\eta } $ is the orbit closure of the characteristic function of the set of 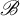 $ \mathscr {B} $-free integers. We show that many results about invariant measures and entropy, previously only known for the hereditary closure of
$ \mathscr {B} $-free integers. We show that many results about invariant measures and entropy, previously only known for the hereditary closure of 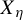 $ X_{\eta } $, have their analogues for
$ X_{\eta } $, have their analogues for 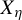 $ X_{\eta } $ as well. In particular, we settle in the affirmative a conjecture of Keller about a description of such measures [G. Keller. Generalized heredity in
$ X_{\eta } $ as well. In particular, we settle in the affirmative a conjecture of Keller about a description of such measures [G. Keller. Generalized heredity in 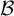 $\mathcal B$-free systems. Stoch. Dyn. 21(3) (2021), Paper No. 2140008]. A central assumption in our work is that
$\mathcal B$-free systems. Stoch. Dyn. 21(3) (2021), Paper No. 2140008]. A central assumption in our work is that 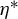 $\eta ^{*} $ (the Toeplitz sequence that generates the unique minimal component of
$\eta ^{*} $ (the Toeplitz sequence that generates the unique minimal component of 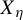 $ X_{\eta } $) is regular. From this, we obtain natural periodic approximations that we frequently use in our proofs to bound the elements in
$ X_{\eta } $) is regular. From this, we obtain natural periodic approximations that we frequently use in our proofs to bound the elements in 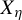 $ X_{\eta } $ from above and below.
$ X_{\eta } $ from above and below.
Keywords
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 2
- Cited by


