Introduction
The traditional approach for producing snow specimens for laboratory experiments is to collect intact samples from the field (Reference Flin, Brzoska, Lesaffre, Coléou and PieritzFlin and others, 2004; Reference Kaempfer and SchneebeliKaempfer and Schneebeli, 2007), which are subject to the entire variability of natural snow. Despite predominant crystal habits in a particular snowfall, shapes can differ significantly due to changes in atmospheric conditions during growth. In addition, collecting natural snow samples requires additional effort for sample casting (Reference Heggli, Frei and SchneebeliHeggli and others, 2009) and transport and rather limits experiments to cold regions with sufficient amounts of snowfall. Similarly to other material science disciplines it would be desirable to produce well-conditioned, aggregated (i.e. sintered) snow samples with controlled microstructural characteristics in the laboratory (Reference Tanikawa, Aoki, Hori, Hachikubo, Abe and AniyaTanikawa and others, 2006). In particular, recent experiments with high-resolution microcomputer tomography demand better control of snow microstructure with reproducible characteristics of initial density and specific surface area (Reference Schleef and LöweSchleef and Löwe, 2013).
A common way to create artificial snow is to spray water droplets into liquid nitrogen, a procedure which was used by Kingery (1960); machines based on this idea have been described by, for example, Sommerfield and Freeman (1988). The material resembles technical snow produced by freezing water droplets from snow lances or guns for ski pistes. Freezing droplets in liquid nitrogen yield reproducible ice particles but, due to the large, rounded grain shapes, this snow type reduces interfacial coarsening effects. Snow coarsening is, however, an essential feature of natural snow, demanding more-realistic constituent particles similar to atmospherically grown crystals, such as dendrites, needles, columns or plates, which are grown from vapor. These complex crystal shapes lead to much lower aggregate densities and structural correlations during deposition (Reference Löwe, Egli, Bartlett, Guala and ManesLöwe and others, 2007). The crystal habit depends mainly on the degree of supersaturation and the temperature, which is described and visualized in the morphology diagram of Nakaya (Reference NakayaNakaya, 1954; Reference LibbrechtLibbrecht, 2005). (Detailed descriptions of snow formation are given by, for example, Vali (1996), Pruppacher and others (1998) and Reference Armstrong and BrunArmstrong and Brun (2008).)
The idea of reproducing cloud processes in the laboratory by nucleation of ice crystals in supersaturated air is quite old, and a significant body of work has been devoted to crystal growth in diffusion chambers (Reference Nakaya, Satô and SekidoNakaya and others, 1938; Reference Hallett and MasonHallett and Mason, 1958; Reference Lamb and ScottLamb and Scott, 1972; Reference Sato and KikuchiSato and Kikuchi, 1985). These devices were optimized to control and measure growth velocities and crystal habits of individual ice crystals in supersaturated vapor. Due to the focus on individual crystals, only very small amounts of snow were commonly produced. In contrast, Breilling and others (2012) built a machine to produce dendritic snow in streams of cold and moist air, with the focus on the production of large amounts of powder snow for ski pistes. Their device is, however, not designed to produce snow crystals of sufficient quality to conduct laboratory experiments on the snow microstructure. A suitable idea for nature-like snow production came from Nakamura (1978), who built a machine called a frost box, where snow crystals grow on wires in a stream of supersaturated air.
Following this idea, we built a machine called a snowmaker. A first simple wooden prototype was built and operated several years ago, as described by Meier (2006). Following this initial design, a similar device was built by Reference Bones, Adams, Schweizer and Van HerwijnenBones and Adams (2009). Based on the prototype, we designed an improved device for permanent operation in a cold laboratory with minimal maintenance. Several kilograms of nature-identical snow can be produced each day. Compared to the prototype, the control parameters can be adjusted with higher precision. In previous devices, snow crystals were removed from the wires either by manual shaking of the box or by an automatic vibration mechanism. In contrast, our new design enables complete removal of the crystals at specific time-steps and, therefore, promotes similar growth conditions after each removal. The present paper aims to characterize the technical particulars and limitations of the newly designed snowmaker for producing a large number of crystals, that are well suited to generate sintered samples with varying crystal habits and micro-structural characteristics that resemble natural snow. The design seeks to minimize moisture discharge in the cold laboratory and to simplify mandatory defrosting cycles by using a modular assembly system. The design is based on engineering drawings, which can be provided upon request for further development.
The paper is organized as follows. First we present a detailed description of the machine. In the results section, we present experiments to demonstrate its operational parameters, analyze the microstructure and the crystal shapes of the produced snow, and make a comparison with natural snow. Next the results and limitations are discussed, and a summary and conclusions are provided in the final section.
Design
The basic principles of the snowmaker follow the idea of Nakamura (1978). A schematic of our design is shown in Figure 1. In a laboratory at about –20°C, a water basin is heated to ~30°C. The basin is insulated and closed by a similarly insulated cover. At one side of the cover a cross-flow fan blows the cold air of the laboratory below the cover across the water surface. Heating the water leads to intense evaporation at the water surface. The moist air is kept below the cover of the basin and can only leave it through a flow channel on the side opposite to the fan. After the flow channel the air enters a second chamber where it rises and cools. This configuration leads to supersaturation of the air.

Fig. 1. Sectional drawing of the snowmaker. The gray arrows indicate the flow of the airstream.
Nylon wires are stretched across this second chamber to promote nucleation of the supersaturated air (hence, we refer to it as the nucleation chamber). Ice crystals grow on the wires (Fig. 2); this is similar to snow crystals in clouds, where nucleation is caused by aerosols. A difference is that the crystals on the wires grow mainly downwards against the direction of the airstream and not in every direction uniformly. At regular (e.g. hourly) time intervals, a brush rack moves across the wires and breaks off the ice crystals, which fall as snowflakes into a box at the bottom of the nucleation chamber. The air leaves the nucleation chamber at the top and reaches a moisture trap that is made of simple fabric (mesh size 0.2 mm), causing the remaining moisture to deposit. As a consequence, there is no release of moist air into the laboratory. A side door in the nucleation chamber allows visual examination of the inside. The snow can be taken from the box.

Fig. 2. Crystal growth on nylon wires in the nucleation chamber.
The structural supports are aluminum and the walls of the nucleation chamber are polycarbonate plates. The water basin and its cover are made of aluminum plates, which are insulated by 3 cm thick Styrofoam surrounded by polystyrol plates on the outside. The surface area of the water is ~80 x 60 cm2, with ~15 cm water depth. A small opening at the top of the cover provides access for refilling the water through a pipe which ends below the water surface and can be closed by a plug. We used filtered and deionized water to minimize deposits in the basin. The flow channel is also insulated and heated by self-regulating heating wires to a temperature of just above 0°C. This configuration prevents snow or ice formation from the moist air before reaching the nucleation chamber and guarantees an invariant airstream. The flow channel expands and rises to the nucleation chamber to direct the airflow to the wires. About 400 nylon wires of 0.6 mm diameter are stretched across an area of ~80 x 60 cm2 and a height of ~70 cm. The brush rack (motor-driven) is guided by two linked linear bearings (igus DryLin ZLW Toothed belt axis) mounted at the top of the side-walls of the nucleation chamber. The bearings are specially designed for use at freezer temperatures. A brush cycle always includes back and forth motion of the rack. On standby, the rack is placed at the front wall outside the airstream.
An electronic box is mounted at the side of the water basin and contains the controls and supplies of all the electronic components. The water temperature is continuously measured by a sensor (Pt 1000) to trigger (JUMO di eco digital meter) a heater coil (wisag IMI-KMV mineral-insulated heating pipeline, 1760 W) and maintain a constant temperature. A motor (Schumacher & Burkhardt three-phase electric motor, 0.18 kW at 1380 rpm) which drives the cross-flow fan (ebm-papst QLZ06) can be set to the desired speed (Optidrive frequency inverter). The speed and interval of the brush rack motor (igus NEMA23 two-phase hybrid motor) are usually fixed. They can be changed by connecting the motor to a computer (Nanotec motor controller).
The entire construction can be separated into three parts: the water basin with the electronic box and the fan, the nucleation chamber including the flow channel and the snow box, and the moisture trap. The moisture trap can easily be carried out of the laboratory, while the other parts are placed on rollers and can be pushed out. Each part is dimensioned such that it fits through a 90 cm wide laboratory door. The parts can then be defrosted and dried without defrosting the laboratory.
Results
Operation
The snowmaker in operation is shown in Figure 3. To determine the technical specification of the device and provide a detailed analysis of the type and quality of the snow produced, we conducted a series of experiments. In principle, all of the following parameters could be adjusted: the temperature of the laboratory, T lab; the temperature of the water, T water; the speed of the cross-flow fan; and the frequency of crystal removal by the brush rack.

Fig. 3. Snowmaker in operation in the cold laboratory.
The frequency of the brush rack sets the growth duration and determines the maximum size of the crystals. This is of minor importance for our applications, because the maximum crystal size is determined afterwards by sieving. Therefore we used a fixed value of one rack drive per hour.
The speed of the cross-flow fan determines the flow field inside the snowmaker. Here it is necessary to find a compromise between high velocities for a sufficient mass supply and low velocities to achieve a steady airstream over all the wires and to avoid large perturbations of the growing crystals due to the airflow. To this end, we measured the flow velocity, v, in the snowmaker, with a MiniAir 20 device from Schiltknecht. Measured velocities were averaged over at least 10 s from two independent measurements. As a result of these tests we adjusted the fan such that the flow velocity directly after the fan was v ≈ 3.8 m s−1. For these settings the velocity drops to ~1.8 m s−1 in the flow channel and to almost vanishing velocities of 0–0.4 m s−1 in the nucleation chamber.
In the following, we thus concentrate on various combinations of the two main parameters, T
lab and T
water, which have a major influence on the operation and the resulting snow. Henceforth we refer to a particular combination of temperatures as T
lab/T
water. For each combination we ran the snowmaker for 24 hours, after a several-hour initialization period. Occasionally, complete defrosting of the device was required. Within the 24 hours of each experiment the machine was operated with minimum disturbance from human cold-laboratory access and without water refill. Directly after the experiment the following parameters were measured: the water loss, ![]() , in the basin (accuracy ±1 L), the mass, m, of the produced snow in the box (±0.1 kg m−3) and the approximate volume, V, of the snow in the box (±0: 02 m3). The last parameter could not be measured exactly because the surface of the snow in the box is not planar and its grading led to densification. From these parameters the efficiency of snow production was calculated as the ratio of water loss to produced snow mass (±5%). An approximate density (±10 kg m−3) was calculated from the volume and the mass of snow in the box. All results are listed in Table 1.
, in the basin (accuracy ±1 L), the mass, m, of the produced snow in the box (±0.1 kg m−3) and the approximate volume, V, of the snow in the box (±0: 02 m3). The last parameter could not be measured exactly because the surface of the snow in the box is not planar and its grading led to densification. From these parameters the efficiency of snow production was calculated as the ratio of water loss to produced snow mass (±5%). An approximate density (±10 kg m−3) was calculated from the volume and the mass of snow in the box. All results are listed in Table 1.
Table 1. Results of experiments with different settings of laboratory temperature, T
lab, and water temperature, T
water, for 24 hours. T
nuc is the averaged temperature in the nucleation chamber. Water loss in the basin, ![]() , snow mass, m, and volume, V, in the box and the resulting values for snow density, ρ
box, in the box and the efficiency as the relation of water loss to snow mass are listed. ρ
CT and SSA (specific surface area) are the results from the µCT scans. The rightmost column gives the classification number (Magono and Woo Reference Magono and Woo LeeLee, 1966). The experiment marked with * is a repeat of the experiment listed above
, snow mass, m, and volume, V, in the box and the resulting values for snow density, ρ
box, in the box and the efficiency as the relation of water loss to snow mass are listed. ρ
CT and SSA (specific surface area) are the results from the µCT scans. The rightmost column gives the classification number (Magono and Woo Reference Magono and Woo LeeLee, 1966). The experiment marked with * is a repeat of the experiment listed above

As expected, the water loss increases with increasing water temperature. In contrast, the laboratory temperature only has a minor influence on water loss, as shown in Figure 4, where the water loss is plotted against the temperatures of water and laboratory. The data can be empirically fitted by a function ![]() , with parameters A = 3.29, B = –0.27, C = –0.33, D = 0.01 and E = 0.02 (R2 = 0.995). Furthermore, the mass of produced snow increases significantly with higher water temperatures, but at the same time a lower laboratory temperature causes a lower density and, therefore, a higher volume of snow. For water temperatures of 40°C, almost one-third of the water is converted to snow, but the highest efficiency of ~40% is reached with the setting –25°C/+30°C. These values might even be increased if the snow crystals grown in the moisture trap were also used. These moisture-trap crystals are only recommended for experiments with low requirements on microstructure and homogeneity. Note that only for the highest water temperatures of 40°C does some frost start to form in the laboratory and our moisture trap seem to be insufficient.
, with parameters A = 3.29, B = –0.27, C = –0.33, D = 0.01 and E = 0.02 (R2 = 0.995). Furthermore, the mass of produced snow increases significantly with higher water temperatures, but at the same time a lower laboratory temperature causes a lower density and, therefore, a higher volume of snow. For water temperatures of 40°C, almost one-third of the water is converted to snow, but the highest efficiency of ~40% is reached with the setting –25°C/+30°C. These values might even be increased if the snow crystals grown in the moisture trap were also used. These moisture-trap crystals are only recommended for experiments with low requirements on microstructure and homogeneity. Note that only for the highest water temperatures of 40°C does some frost start to form in the laboratory and our moisture trap seem to be insufficient.
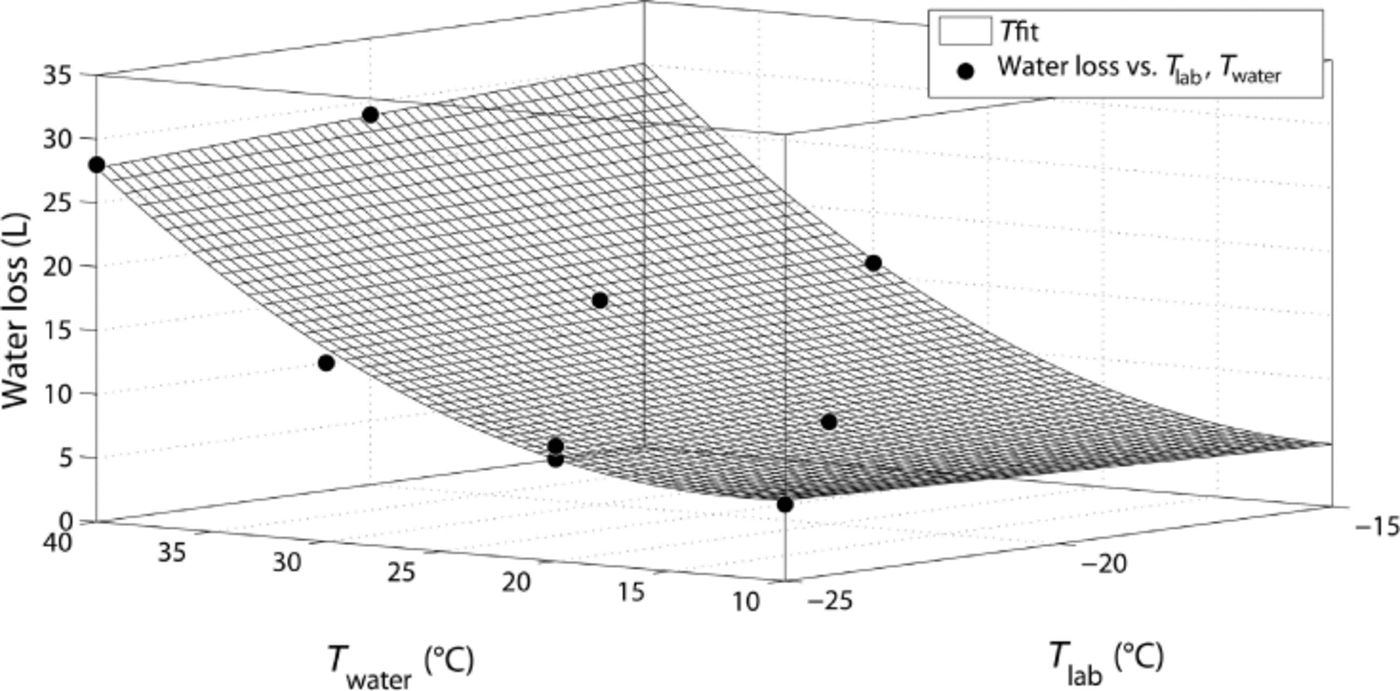
Fig. 4. Water loss vs water temperature and laboratory temperature, together with a surface fit.
For the subsequent interpretation of crystal habits in view of the Nakaya diagram, we also measured the actual temperature in the vicinity of the wires using two temperature sensors (iButton devices). One was attached just below the wires near the back wall of the nucleation chamber, and the other was placed at the air outlet just above the wires. Measured temperatures above the wires are on average 2°C below the lower temperature, due to the cooling of the air as it rises through the chamber. The fluctuations of temperature during the experiments are ~0.5°C superimposed by short temperature rises of up to 4°C every 5 hours, caused by the defrosting cycles of the laboratory generator. Irregular growth of snow sometimes occurs on the temperature sensors, which implies an additional uncertainty in the measurements. A nominal temperature, T nuc, was calculated by averaging over both measurements and the entire experiment time. The values are given in Table 1. Despite the uncertainties, T nuc gives a better estimate of the temperature close to the growing crystals, which can strongly differ from the cold laboratory temperature. The temperature in the chamber, T nuc, can be reasonably well described by a linear combination of water and laboratory temperatures as shown in Figure 5. A simple fit can be given in the form T nuc = a + b Tlab + c Twater. The resulting parameters are a = –4.16, b = 0.76 and c =0.31 (R2 = 0.983).

Fig. 5. Averaged temperature in the nucleation chamber vs water temperature and laboratory temperature, together with a linear surface fit.
Snow microstructure from microcomputer tomography
To analyze the microstructure of the produced snow, three-dimensional microcomputer tomographic (µCT) images were taken. Snow from the box was sieved into sample holders of 18 mm diameter and adjusted to a height of 15 mm. Each time, two identical samples were prepared to estimate sample-to-sample fluctuations. The samples were stored in a freezer at –60°C to preserve the microstructure until each measurement could be made. The scans were done with a resolution of 10 µm, and a cubic volume of 6.3 mm edge length was analyzed. From the reconstructed images, density and specific surface area (SSA) were calculated, which are considered to be two main micro-structural characteristics of snow. For further details of the scanning and evaluation procedure refer to Schleef and Löwe (2013), who conducted the measurements in the same way. The results are listed in Table 1, where the values correspond to an average over the two samples of the same experiment. The sample-to-sample variations are small. The densities differ for most experiments by only 2 kg m−3. Some experiments, especially experiments –25°C/+20°C and –25°C/+30°C, show higher density differences of up to 10 kg m−3. These are the experiments with the lowest measured densities, so the scanned volume might be insufficiently large to suppress natural volume fraction fluctuations. The sample-to-sample differences of the SSA are only up to 2 mm−1. For the experiment –20°C/+30°C only, a difference of 10 mm−1 was measured. This might be due to the highly irregular crystal shapes at this temperature setting, as described in the next subsection.
Crystal habit from photography
The snow crystals were photographed to characterize the crystal habit. Similarly to the preparation for the µCT, a few crystals from each experiment were sieved in a Petri dish. For each temperature combination, photographs of 10–20 crystals were taken, the most typical of which are shown in Figure 6. Depending on the temperature settings different crystal shapes are produced, which can be related to the natural crystal shapes described in the classification of natural snow crystals according to Magono and Woo Lee (1966). An inherent characteristic of the production method is that crystals break, either during harvest by the brush rack or during the subsequent sieving. The broken branches or pieces are, however, still amenable to classification in terms of the described undamaged natural crystals. For –25°C/+20°C fern-like crystals (classification number: P1f) grow. At –25°C/+30°C, similar crystals are produced, which can also be classified as fern-like or ordinary dendritic (P1e). At –20°C/+20°C and –25°C/+10°C the shapes are more plate-like, and can be described as broad branches (P1c) or dendritic crystals with sector-like ends (P2d). For –20°C/+30°C, quite irregular crystal shapes with a mixture of hollow columns (C1f) and irregular germs (G6) are obtained. At settings –15°C/+30°C, –25°C/+40°C and –20°C/+40°C crystals grow which can be most closely classified as bundles of elementary needles (N1b), with slightly thicker needles at –25°C/+40°C.

Fig. 6. Photographs of snow crystals; the temperature settings (laboratory temperature/water temperature) are indicated. Magnification is the same for all photographs.
For almost all settings, there are clearly dominant crystal types, even though the temperature in the area of nucleation is not perfectly stable and uniform. Observed temperature fluctuations of < 2°C seem not to affect the dominant crystal type. To interpret the observed types at different settings in view of the Nakaya diagram, we consider the temperature, T
nuc, in the nucleation chamber (Table 1) as the relevant parameter. The second parameter is the supersaturation, which could not be measured directly. We could, however, obtain a gross estimate of the supersaturation as follows. The rate of air supply can be calculated from the measured air velocity, v, directly after the cross-flow fan and the area, A ≈ 0.025 m2, of the fan as ![]() . Water vapor is supplied to the incoming airflow at a rate which can be computed from the water loss,
. Water vapor is supplied to the incoming airflow at a rate which can be computed from the water loss, ![]() , in the basin. The vapor concentration in the incoming air can be neglected when compared with
, in the basin. The vapor concentration in the incoming air can be neglected when compared with ![]() , even at saturation, due to the low laboratory temperature. Hence, we can calculate an average concentration of vapor, ρvapor, in the airstream as
, even at saturation, due to the low laboratory temperature. Hence, we can calculate an average concentration of vapor, ρvapor, in the airstream as

with the density of water ρwater ≈ 1000 kg m−3. The gas is cooled to a temperature T
nuc in the vicinity of the wires. If we assume that the wires and the crystals are at the same temperature, the equilibrium vapor pressure of ice, p
eq(T
nuc), can be calculated from the Magnus formula (WMO, 2008), and in turn the equilibrium concentration, ρeq(Tnuc) from the ideal gas law ![]() , with
, with ![]() the molar mass of water, R the gas constant and
the molar mass of water, R the gas constant and ![]() the temperature (K). Eventually we define a supersaturation,
the temperature (K). Eventually we define a supersaturation,
Equation (2) gives a rough estimate of the excess vapor, which is solely computed from experimentally measured parameters. The morphology diagram obtained from the snow-maker (Fig. 7) is thus in reasonable agreement with the Nakaya diagram (Reference NakayaNakaya, 1954; Reference LibbrechtLibbrecht, 2005): the settings –25°C/+30°C and –25°C/+20°C give low temperatures of about 14°C and 18°C and we get dendrites; the settings –20°C/+20°C and –25°C/+10°C cause a lower super-saturation at similar low temperatures, and sectored plates grow; both settings with a water temperature of 40°C and the settings 15°C/+30°C cause temperatures higher than 10°C in the nucleation chamber, leading to the growth of needles, and at a similar temperature but lower supersaturation at the settings –20°C/+30°C hollow columns appear.

Fig. 7. Morphology diagram based on the estimated supersaturation,, and the measured temperature in the nucleation chamber. The classification is indicated, together with parts of the snow crystals.
Interestingly, for some crystals the onset of riming is clearly visible. Usually riming is avoided if the fresh air intake of the laboratory is switched off. Then the air is very clean, especially if the laboratory has already operated for some days. If the production of rimed crystals is desired, the fresh air intake can be permanently switched on. This causes a supply of dust particles or other impurities and, in turn, the enhanced nucleation of water drops and riming on the snow crystals. A rimed, dendritic snow crystal is shown in Figure 8.

Fig. 8. Rimed dendritic snow crystal produced with the snowmaker with fresh air supplied from outside.
Comparison with natural snow
To establish whether snowmaker snow can be used in experiments intended to simulate natural conditions, it is important to compare the obtained crystals with natural snow. To this end, we gathered natural samples of new snow for the main snowfall events in Davos, Switzerland, during the 2011/12 and 2012/13 winters, and sieved and analyzed them in the same way as for the snowmaker samples. The results vary between different snowfall events, but the µCT values of density, 50–110 kg m−3, and SSA, 60–100 mm−1, are in the same range as for most of the snowmaker samples. Especially for the dendritic snowmaker snow with low density and high SSA values, similar results for natural snow samples are quite common. To compare the crystal shapes we analyzed the photographs. In natural snow, stellar shapes occur quite often. This crystal type cannot be produced with the snowmaker, since the nucleation seeds have to be in the center of the stars. In the snowmaker the wires play the role of the nucleation seed from which the crystals are broken. Directionality in growth is added by the upward airflow (Fig. 2). However, in most of our natural snow samples, only individual branches of stellar dendrites appear, either as a consequence of sieving or of wind-induced fragmentation during snowfall. These branches compare well with the dendrites produced with the snowmaker at settings –25°C/+20°C or –25°C/+30°C. As shown in Figure 9, the size and morphology of the crystals is identical. For these samples also the µCT results show that densities differ by 20 kg m−1 (~60 kg m−1 for snowmaker snow vs ~80 kg m−3 for natural snow) and the SSA is identical, 75 mm−1. In this respect, the sieved natural snow samples are very similar to the dendritic snowmaker snow samples in the measured parameters.

Fig. 9. Photograph of sieved natural snow (top) in comparison with sieved dendritic snowmaker snow (bottom).
Discussion
Similarly to previous devices (the original ‘frost box’; Reference NakamuraNakamura, 1978), our snowmaker is able to produce different kinds of new snow in the laboratory. However, our construction facilitates almost automatic snow production with little manual intervention, once the parameters have been set. The new method of scraping crystals from the wires with a brush rack enables better control of the duration of crystal growth; after each brush run the wires are completely defrosted, leading to invariant initial conditions and growth duration for each growth cycle. The amount of snow production (a few kilograms per day) is sufficient not only for small samples (e.g. for µCT measurements) but also for larger laboratory experiments at the scale of natural seasonal snow cover.
It is important to have sufficiently low laboratory temperatures and high water temperatures to promote crystal growth. A more detailed analysis of the growth conditions requires an estimate of the supersaturation at the nylon wires, which is difficult to measure directly (Reference NakayaNakaya, 1954). However, a rough estimate of the available water mass per air volume could be given solely from experimentally measured quantities, namely the inflow air velocity and water loss. These parameters can be used to compare the obtained crystals with those in the morphology diagram (Reference NakayaNakaya, 1954; Reference LibbrechtLibbrecht, 2005). Though absolute values in Figure 7 cannot be regarded as the true supersaturation, due to negative values, their relative location and the obtained morphology regions in the diagram are consistent with Reference NakayaNakaya, (1954) and Libbrecht (2005). The two main shapes are needles and dendrites. Both types lead to clearly different structural parameters if analyzed with µCT. For needles we obtain densities of ~110 kg m−3 and an SSA of ~60 mm−1 whereas dendrites result in samples with densities of ~60 kg m−3 and an SSA of ~75 mm−1. These different crystal types might be used for experiments which require different snow samples (e.g. to analyze the influence of their different, initial microstructural characteristics on metamorphism or mechanical stability, as required by Schleef and Löwe (2013)).
An important factor in reducing uncertainties in laboratory experiments is reproducibility of the snow crystals. To investigate this, we repeated the experiment with the settings –25°C air temperature and +20°C water temperature after complete defrosting of the device and the laboratory. This experiment is marked with an asterisk in Table 1. The two experiments under the same conditions are consistent with respect to all measured parameters. Small differences are acknowledged, due to the limited measurement accuracy specified in the results section. For the µCT measurements, the differences between the density and SSA for the two experiments are within the measurement accuracy, and the images of the two experiments display identical crystal morphologies. Sample-to-sample fluctuations are small (4 kg m−1 for density and 2 mm−1 for SSA).
By comparison with natural snow, we have also shown that there are natural samples that have the same crystal shapes as our snow and which coincide in the key microstructural parameters, density and SSA. We have demonstrated this agreement between natural and artificial dendritic snow only for sieved snow samples. Sieving is a common method of sample preparation for microstructural experiments (Reference Kaempfer and SchneebeliKaempfer and Schneebeli, 2007; Reference Satyawali, Singh, Dewali, Kumar and KumarSatyawali and others, 2008; Reference Schleef and LöweSchleef and Löwe, 2013). The question remains whether natural snowpacks display other structural characteristics beyond SSA and density, that cannot be reproduced from artificial snow in the laboratory where sieving is involved. Sieving probably destroys potential aggregation effects that might build up in real snowflakes (Reference Westbrook, Ball and FieldWestbrook and others, 2006) in the atmosphere. Likewise, deposition effects (Reference Löwe, Egli, Bartlett, Guala and ManesLöwe and others, 2007) will change under fragmentation of the crystals, since sieving reduces the particle size. This change is confirmed by comparing the snow density measured in the box (ρbox; Table 1) with the µCT density (ρCT; Table 1) obtained after sieving. Note that both densities show the same trend but the µCT density is generally higher, due to the sieving. The fact that a low snow production, as for settings –20°C/+20°C and –20°C/+30°C, coincides with high densities is also due to smaller crystal sizes obtained for slower growth. In principle, such an influence could be further investigated by changing the brush rack frequency and thereby the crystal size.
Finally, we note that for all settings leading to a snow production of at least 0.05 m3 d−1, the stable operation of the snowmaker requires the brush rack to be cleared of ice and snow at least twice a day. Cleaning can be done without disturbing the production. Also for the highest water temperatures of 40°C the operation of the device for several days can cause the growth of ice drops at the wires that are not scraped off by the brush rack. These ice drops do not occur at lower water temperatures and can easily be avoided at higher water temperatures by regular defrosting. In addition, for most settings the box catching the snow fills up after 1–2 days.
Conclusions
We have built an improved machine, which requires only minimum maintenance, to produce nature-identical snow in the laboratory. The transformation of water into snow of high quality reaches ~40%. The overall snow production of ~0.1 m3 d−1 is well suited to both small and large laboratory experiments. Depending on the settings, it is possible to obtain different crystal habits, which are consistent with the morphology diagram. As an advantage over previous designs or the collection of natural snow samples, we can generate reproducible samples under well-defined conditions. The snowmaker snow is more homogeneous than most natural snow samples, since laboratory conditions are almost constant while natural conditions often vary during snowfall events. Also the temperature in the laboratory is significantly lower than typical temperatures during snowfall in the field. As a result, our snow is less influenced by structural changes that are strongly temperature-dependent. This control allows the production of nature-identical snow and, from that, the generation of sintered snow samples. Thereby, microstructural characteristics of SSA and density vary with crystal habit and allow for reproducible, high-resolution µCT experiments.
Acknowledgements
This work was funded by the Swiss National Science Foundation (SNSF) through grant No. 200021_132549. We gratefully acknowledge the contributions of M. Meier, J. Spiegel and J. Graupeter to the development of snowmaker I.












