Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T06:43:05.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Cardinal collapsing and ordinal definability

Published online by Cambridge University Press:  12 March 2014

Petr Štěpánek
Petr Štěpánek*
Affiliation:
Department of Cybernetics and Operational Research, Charles University, Prague 118 00 Praha 1, Czechoslovakia
Get access Rights & Permissions [Opens in a new window]

Extract

We shall describe Boolean extensions of models of set theory with the axiom of choice in which cardinals are collapsed by mappings definable from parameters in the ground model. In particular, starting from the constructible universe, we get Boolean extensions in which constructible cardinals are collapsed by ordinal definable sets.

Let 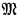be a transitive model of set theory with the axiom of choice. Definability of sets in the generic extensions of 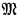is closely related to the automorphisms of the corresponding Boolean algebra. In particular, if G is an 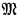-generic ultrafilter on a rigid complete Boolean algebra C, then every set in 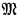[G] is definable from parameters in 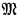. Hence if B is a complete Boolean algebra containing a set of forcing conditions to collapse some cardinals in 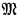, it suffices to construct a rigid complete Boolean algebra C, in which B is completely embedded. If G is as above, then 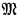[G] satisfies “every set is 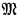-definable” and the inner model 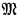[G ∩ B] contains the collapsing mapping determined by B. To complete the result, it is necessary to give some conditions under which every cardinal from 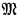[G ∩ B] remains a cardinal in 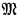[G].

The absolutness is granted for every cardinal at least as large as the saturation of C. To keep the upper cardinals absolute, it often suffices to construct C with the same saturation as B. It was shown in [6] that this is always possible, namely, that every Boolean algebra can be completely embedded in a rigid complete Boolean algebra with the same saturation.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 4 , December 1978 , pp. 635 - 642
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Engelking, R. and Karlowicz, M., Some theorems of set theory and their topological consequences, Fundamenta Mathematlcae, vol. 57 (1965), pp. 275–285.CrossRefGoogle Scholar
[2]Erdös, P. and Rado, R., Intersection theorems for systems of sets, Journal of the London Mathematical Society, vol. 35 (1960), pp. 85–90.CrossRefGoogle Scholar
[3]McAloon, K., Consistency results about ordinal definability, Annals of Mathematical Logic, vol. 2 (1971), pp. 449–467.CrossRefGoogle Scholar
[4]Shelah, S., Why there are many non isomorphic models for unsuperstable theories, Proceedings of the International Congress of Mathematicians, Vancouver, 1974, Canadian Mathematical Congress, 1975, pp. 553–557.Google Scholar
[5]Stavi, J., On cardinal collapsing with reals, Israel Journal of Mathematics, vol. 18 (1974), pp. 11–18.CrossRefGoogle Scholar
[6]Štěpánek, P. and Balcar, B., Embedding theorems for Boolean algebras and consistency results on ordinal definable sets, this Journal, vol. 42 (1977), pp. 64–76.Google Scholar
[7]Vopěnka, P. and Hajek, P., The theory of semisets, North-Holland, Amsterdam, 1972.Google Scholar