Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T16:43:56.162Z Has data issue: false hasContentIssue false
  • English
  • Français

THE NUMBER OF PROFINITE GROUPS WITH A SPECIFIED SYLOW SUBGROUP

Part of: Representation theory of groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  19 January 2015

COLIN D. REID
COLIN D. REID*
Affiliation:
University of Newcastle, School of Mathematical and Physical Sciences, University Drive, Callaghan NSW 2308, Australia email colin@reidit.net
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 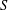$S$ be a finitely generated pro-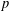$p$ group. Let 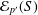${\mathcal{E}}_{p^{\prime }}(S)$ be the class of profinite groups 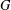$G$ that have 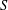$S$ as a Sylow subgroup, and such that 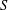$S$ intersects nontrivially with every nontrivial normal subgroup of 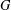$G$. In this paper, we investigate whether or not there is a bound on 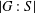$|G:S|$ for 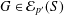$G\in {\mathcal{E}}_{p^{\prime }}(S)$. For instance, we give an example where 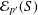${\mathcal{E}}_{p^{\prime }}(S)$ contains an infinite ascending chain of soluble groups, and on the other hand show that 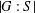$|G:S|$ is bounded in the case where 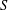$S$ is just infinite.

Keywords

profinite groupsSylow theory

MSC classification

Primary: 20E18: Limits, profinite groups
Secondary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 1 , August 2015 , pp. 108 - 127
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Aschbacher, M., Finite Group Theory (Cambridge University Press, New York, 2000).CrossRefGoogle Scholar
Craven, D. A., Fusion Systems: An Algebraic Approach (Cambridge University Press, Cambridge, 2011).CrossRefGoogle Scholar
Feit, W. and Thompson, J. G., ‘Solvability of groups of odd order’, Pacific J. Math. 13 (1963), 775–1029.CrossRefGoogle Scholar
Gagola, S. M. Jr. and Isaacs, I. M., ‘Transfer and Tate’s theorem’, Arch. Math. (Basel) 91(4) (2008), 300–306.CrossRefGoogle Scholar
Gilotti, A. L., Ribes, L. and Serena, L., ‘Fusion in profinite groups’, Ann. Mat. Pura Appl. (4) 177 (1999), 349–362.CrossRefGoogle Scholar
Leedham-Green, C. R. and McKay, S., The Structure of Groups of Prime Power Order (Oxford University Press, New York, 2002).CrossRefGoogle Scholar
Reid, C. D., ‘Finiteness properties of profinite groups’, PhD Thesis, University of London, 2010.Google Scholar
Reid, C. D., ‘The generalised pro-fitting subgroup of a profinite group’, Comm. Algebra 41(1) (2013), 294–308.CrossRefGoogle Scholar
Rose, J. S., A Course on Group Theory (Cambridge University Press, Cambridge, 1978).Google Scholar
Stancu, R. and Symonds, P., ‘Fusion systems for profinite groups’, 2012, arXiv:1204.2582.Google Scholar
Stather, M., ‘Constructive Sylow theorems for the classical groups’, J. Algebra 316(2) (2007), 536–559.CrossRefGoogle Scholar
Symonds, P., ‘On cohomology isomorphisms of groups’, J. Algebra 313(2) (2007), 802–810.CrossRefGoogle Scholar
Tate, J., ‘Nilpotent quotient groups’, Topology 3(Suppl. 1) (1964), 109–111.CrossRefGoogle Scholar
Yoshida, T., ‘Character-theoretic Transfer’, J. Algebra 52 (1978), 1–38.CrossRefGoogle Scholar
Zassenhaus, H., ‘Beweis eines Satzes über diskrete Gruppen’, Abh. Math. Semin. Univ. Hambg. 12 (1938), 289–312.CrossRefGoogle Scholar