Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-12T12:11:31.902Z Has data issue: false hasContentIssue false
  • English
  • Français

One-relator groups that are residually of prime power order

Published online by Cambridge University Press:  09 April 2009

D. Gildenhuys
D. Gildenhuys
Affiliation:
Department of Mathematics, McGill University, Montreal 110, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If C is a class of groups, we denote by RC the class of groups which are residually in C i.e. G ∈ RC if and only if 1 ≠ g ∈ G implies that there exists a normal subgroup N of G such that g ∈ N and G/N ∈ C. A group G is residually a finite p-group if it belongs RFp, where Fp denotes the class of finite p-groups. One also says that the groups in RFp are residually of order equal to a power of the prime p. Given a group G with one defining relator r, one might ask for conditions on the “form” of the relator that would guarantee that G have certain residual properties. In this context, Baumslag (1971) has proved that if all the exponents of the generators appearing in r are positive, then G is residually solvable. In the same paper he also concerned himself with the residual nilpotence of one-relator groups, and found that the situation there was much more complicated. If one goes one step further and asks for conditions that will ensure that for a given prime p the one-relator group be residually a finite p-group, then very little seems to be known. Of course, if one takes r to be one of the generators: 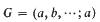then G is freely generated by the remaining generators, and hence is in RFp for all primes p (Mahec (1949), Lazard (1965), 3.1.4). Our main purpose in this paper is to develop methods of generating examples of one-relator groups that are residually of order equal to a given prime p.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 19 , Issue 4 , June 1975 , pp. 385 - 409
Copyright
Copyright © Australian Mathematical Society 1975

References

Baumslag, G. (1964), ‘Groups with one defining relator’, J. Austral. Math. Soc. 4, 385–392.CrossRefGoogle Scholar
Baumslag, G. (1971), ‘Positive one-relator groups’, Trans. Amer. Math. Soc. 156, 156–183.CrossRefGoogle Scholar
Bourbaki, N. (1951), Topologie générale, Chap. III, (Hermann, Paris, 1951).Google Scholar
Gildenhuys, D. (1968), ‘On Pro-p-groups with a single defining relator’, Invent. Math. 5, 357–366.Google Scholar
Gildenhuys, D. (To appear), ‘Amalgamations of pro-p-groups with one defining relator’.Google Scholar
Gildenhuys, D., Lim, C. K. (1972), ‘Free pro-C-groups’, Math. Z. 125, 233–254.CrossRefGoogle Scholar
Gildenhuys, D. and Ribes, L. (1973), ‘A Kurosh subgroup theorem for free pro-C-groups’, Trans. Amer. Math. Soc. 186, 309–329.Google Scholar
Gildenhuys, D. and Ribes, L. (1974), ‘On the cohomology of certain topological colimits of pro-C-groups’, J. Algebra 29, 172–197.CrossRefGoogle Scholar
Gruenberg, K. (1957), ‘Residual properties of infinite solvable groups’, Proc. London Math. Soc. (3) 7, 29–62.CrossRefGoogle Scholar
Higman, G. (1964), ‘Amalgams of p-groups’, J. Algebra 1, 301–305.CrossRefGoogle Scholar
Kennison, J. and Gildenhuys, D. (to appear), ‘Equational completions, model induced triples and pro-objects’, J. Pure Appl. Algebra.Google Scholar
Labute, J. (1967), ‘Algebres de Lie et pro-p-groupes definis par un seule relation’, Invent. Math. 4, 142–158.CrossRefGoogle Scholar
Labute, J. (1967a), ‘Classification of Demushkin groups’, Can J. Math. 19, 106–132.CrossRefGoogle Scholar
Lazard, M. (1965), Groupes analytiques p-adiques, Chap, II. (Publications math. de I'IHES no. 26, 1965).Google Scholar
Magnus, W., Karass, A. and Solitar, D. (1966), Combinatorial Group Theory. (Interscience tracts in Pure and Applied Mathematics, vol. 20, Interscience, New York, 1966).Google Scholar
Malcev, A. (1949), ‘Generalized nilpotent algebras and their associated groups’, Mat. Sb. N. S. 25, (67), 347–66.Google Scholar
Serre, J.-P. (1962/1963), Structure de certains pro-p-groupes. (Seminaire Bourbaki, no. 252, 1962/1963).Google Scholar
Serre, J.-P. (1964), Cohomologie Galoisienne. (Lecture notes in mathematics, no. 5, Berlin-Gottingen-Heidelberg, 1964).Google Scholar
Serre, J.-P. (1970), Cours d'arithmetique. (Presses Universitaires de France, Paris, (1970)).Google Scholar