Article contents
Encoding hybridized institutions into first-order logic
Published online by Cambridge University Press: 12 November 2014
Abstract
A ‘hybridization’ of a logic, referred to as the base logic, consists of developing the characteristic features of hybrid logic on top of the respective base logic, both at the level of syntax (i.e. modalities, nominals, etc.) and of the semantics (i.e. possible worlds). By ‘hybridized institutions’ we mean the result of this process when logics are treated abstractly as institutions (in the sense of the institution theory of Goguen and Burstall). This work develops encodings of hybridized institutions into (many-sorted) first-order logic (abbreviated 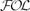 $\mathcal{FOL}$) as a ‘hybridization’ process of abstract encodings of institutions into
$\mathcal{FOL}$) as a ‘hybridization’ process of abstract encodings of institutions into 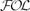 $\mathcal{FOL}$, which may be seen as an abstraction of the well-known standard translation of modal logic into
$\mathcal{FOL}$, which may be seen as an abstraction of the well-known standard translation of modal logic into 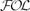 $\mathcal{FOL}$. The concept of encoding employed by our work is that of comorphism from institution theory, which is a rather comprehensive concept of encoding as it features encodings both of the syntax and of the semantics of logics/institutions. Moreover, we consider the so-called theoroidal version of comorphisms that encode signatures to theories, a feature that accommodates a wide range of concrete applications. Our theory is also general enough to accommodate various constraints on the possible worlds semantics as well a wide variety of quantifications. We also provide pragmatic sufficient conditions for the conservativity of the encodings to be preserved through the hybridization process, which provides the possibility to shift a formal verification process from the hybridized institution to
$\mathcal{FOL}$. The concept of encoding employed by our work is that of comorphism from institution theory, which is a rather comprehensive concept of encoding as it features encodings both of the syntax and of the semantics of logics/institutions. Moreover, we consider the so-called theoroidal version of comorphisms that encode signatures to theories, a feature that accommodates a wide range of concrete applications. Our theory is also general enough to accommodate various constraints on the possible worlds semantics as well a wide variety of quantifications. We also provide pragmatic sufficient conditions for the conservativity of the encodings to be preserved through the hybridization process, which provides the possibility to shift a formal verification process from the hybridized institution to 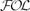 $\mathcal{FOL}$.
$\mathcal{FOL}$.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2014
References
- 23
- Cited by

