1. Introduction
We present an implementation of the basics of universal algebra in univalent foundations within the formal environment of UniMath by Voevodsky et al. (Reference Voevodsky, Ahrens and Grayson2024).
Universal algebra aims to identify common patterns and properties that emerge across different algebraic structures, leading to a deeper understanding of algebraic systems as a whole.Footnote 1 It has strong connections with categorical reasoning and finds applications in several areas of computer science (in database theory and formal methods (Van Horebeek and Lewi, Reference Van Horebeek and Lewi2012)), mathematical logic (mainly, model theory (Chang and Keisler, Reference Chang and Keisler1992)) and cybersecurity (including cryptographic and communication protocols (Dolev and Yao, Reference Dolev and Yao1983)).
Since in all those situations, it is natural to study algebraic structures modulo isomorphism, univalent mathematics is especially suited for formalising universal algebra.
The choice of working within the UniMath environment has appeared natural since it provides a minimalist implementation of univalent type theory. At the same time, the system comes with an extensive repository of mechanised results covering several fields of mathematics. It then opens a wide range of possibilities for future development of our formalisation.
The code surveyed here introduces the central notions concerning multi-sorted signatures. Formally defining all the basics has required a certain care. In particular, we had to introduce heterogeneous vectors and generalise types involving signatures by introducing (what we called) “sorted types”.
Having signatures, we then have given the related formalisation of the category of algebras using the notion of a displayed category by Ahrens and Lumsdaine (Reference Ahrens and Lumsdaine2019) over the category of sorted hSets, whose univalence is proven by adapting the strategy used for the univalence of functor categories. The resulting construction is still a modular one, and the resulting proof term is more concise, for sure, than the one obtained by checking that algebras and homomorphisms satisfy the axioms for standard categories.
We encode terms as lists of operation symbols to be thought of as instructions for a stack-based machine. Terms are those lists of symbols that may be virtually executed without generating type errors or stack underflows.
We show that defining terms this way still yields the expected (homotopy) W-type structure in the single-sorted case. Moreover, we prove that the term algebra over a signature is the initial object in the corresponding category and that, more generally, an algebra of terms over a signature and a set of variables has the desired universal mapping property.
Our formalisation also includes the notion of equations and algebras modelling an equation system associated with a signature; as for the category of algebras, we use the displayed category formalism to construct the univalent category of equational algebras over a given signature
![]() $\sigma$
as the full subcategory of algebras over
$\sigma$
as the full subcategory of algebras over
![]() $\sigma$
satisfying an equation system.
$\sigma$
satisfying an equation system.
Revision history. This work is an expanded version of a prior conference paper (Amato et al., Reference Amato, Maggesi, Parton and Perini Brogi2020) that was presented at the Workshop on Homotopy Type Theory/Univalent Foundations (HoTT/UF) in 2020. An intermediate version appear in the fourth author’s PhD thesis (Perini Brogi, Reference Perini Brogi2022). Modifications encompass a comprehensive overhaul of the presentation along with the addition of new content, most notably, the study of the homotopy W-type structure of our term algebras.
1.1 Goals and methodology
What we have mechanised is not a mathematical novelty, but our endeavour has some payoffs.
On the practical side, the code introduces in the UniMath library a minimal set of definitions and results that is open to the community of developers for future achievements and formal investigations on the relation between pre-categorical research in general algebraic structures and its subsequent development in, e.g., Lawvere theories.
On the technical side, a peculiar feature of our code is the original implementation of term algebras over a signature. We provide a detailed account of the full construction of the term algebra from ground up starting from the inductive type of natural numbers and deriving step-by-step the necessary intermediate structures such as (heterogeneous) vectors and lists.
Incidentally, this aligns well with the coding conventions adopted in the UniMath library: both record and inductive types are avoided to maintain the system’s foundational and philosophical soundness.
Accordingly, one of our main goals has been to make all our constructions about terms evaluable – as far as possible – by the built-in automation mechanisms of the proof assistant. More precisely, we represent each term using a sequence of function symbols. This sequence is thought to be executed by a stack machine: Each symbol of arity
![]() $n$
pops
$n$
pops
![]() $n$
elements from the stack and pushes a new element at the top. A term is denoted by a sequence of function symbols that a stack-like machine can execute without type errors and stack underflow, returning a stack with a single element.
$n$
elements from the stack and pushes a new element at the top. A term is denoted by a sequence of function symbols that a stack-like machine can execute without type errors and stack underflow, returning a stack with a single element.
This approach led us to prove a recursion and induction principle on terms that are evaluable as a functional term of the formal system. This performance is somehow mandatory when adhering to a general constructive and computational approach such as (small scale) reflection (Gonthier and Mahboubi, Reference Gonthier and Mahboubi2010; Beeson, Reference Beeson2016): with our formalised stack machine, we have written in UniMath an implicit algorithm to compute terms over a signature; using our induction principle, we can run it – so to speak – within the very formal system of UniMath and use it to reason about terms safely.
Moreover, our methodology sympathises (in a sense) with the so-called Poincaré principle of Barendregt and Cohen (Reference Barendregt and Cohen2001): our implementation of terms allows us to rely on the very core engine of UniMath when dealing with these formal objects so that whenever we want to handle them, we can focus on the actual demonstrative contents of the formalisation, leaving to the automation behind the computer proof assistant the trivial computational steps involved in the very proof-term.
Generally speaking, standard categorical presentations, though perspicaciously elegant in their abstractness, lack specific suitability for computerised mathematics. By contrast, our goal is justified by a specific need for methodological coherence – we just sketched it a few lines above – when approaching a work in formalisation. Having proof terms that the computational machinery of UniMath practically evaluates as a correctly typed function fits the philosophy and aims of the mechanisation of mathematics better than just giving a formal counterpart of traditional mathematical notions that the computer cannot handle feasibly.
1.2 Paper outline
In what follows, we survey all the notions we introduced in our implementation, structured as an informal presentation of the code; next, we proceed with the discussion of some examples of algebraic structures, to conclude then with some words on future and related work.
In detail, the paper is structured as follows:
-
• In Section 2.1, we introduce some extensions of the UniMath library that are needed in the rest of our work such as general constructions about lists and (heterogeneous) vectors;
-
• In Section 2.2, we formalise the very basics of universal algebra: multi-sorted signatures, their algebras and homomorphisms;
-
• In Sections 2.3, 2.4 and 2.5, we present the main details of our implementation of terms, prove that term algebras and free algebras do have the required universal property – stated as the contractibility of the type of out-going homomorphisms – and discuss the practical and methodological relevance of our induction principle on terms;
-
• In Section 2.6, we discuss how our notion of ground term algebra has the structure of a W-type;
-
• In Section 2.7, we introduce systems of equations and equational algebras over a signature;
-
• In Section 2.8, we sketch the main lines of our constructions of the categories of algebras and equational algebras;
-
• Finally, Section 3 is devoted to three applications of our implementation, namely: lists (Section 3.1), monoids (Section 3.2) and Tarski’s semantics of propositional boolean formulas (Section 3.3).
1.3 Code structure
Our code is part of the official UniMath distribution (Voevodsky et al., Reference Voevodsky, Ahrens and Grayson2024).Footnote 2 The revision discussed in this paper is archived on Software Heritage. To improve readability, in what follows, most proofs and technicalities are omitted, even though they are available in our repository and reachable via the blue hyperlinks in the paper.
The implementation discussed in the present article consists mainly of the files in the directories
-
• UniMath/Algebra/Universal for the basics of universal algebra (together with auxiliary definitions and results) and
-
• UniMath/CategoryTheory/categories/Universal_Algebra for the categories of algebras and equational algebras over a signature.
However, some improvements to the UniMath library not strictly connected to universal algebras have been introduced in the following directories:
-
• UniMath/Combinatorics for vectors, lists and sets with decidable equality;
-
• UniMath/Induction/W for the basic definitions of homotopy W-types.
In order to help readers to browse our library, we summarise the dependencies between the files by the diagram in Figure 1 – where an arrow pointing to a node indicates the dependency of the target from the source.

Figure 1. Intermodule dependencies of the universal algebra formalisation in UniMath.
2. Surveying the code
Before beginning our code survey, we review the fundamentals of univalent reasoning in UniMath and establish consistent notation for the remainder of the paper and accompanying code. The formal system behind UniMath is Martin-Löf type theory extended with Voevodsky’s univalence axiom, which enlightens the homotopic character of equality types. In this framework, propositions and sets are defined homotopically, and we refrain from usin Coq’s native ![]() and
and ![]() universes. Our library employs only the inductive types defined in UniMath’s prelude: sum types, equality types, natural numbers and booleans. This choice is well explained in Bezem et al. (Reference Bezem, Buchholtz, Grayson and Shulman2021), where the authors state:Footnote
3
universes. Our library employs only the inductive types defined in UniMath’s prelude: sum types, equality types, natural numbers and booleans. This choice is well explained in Bezem et al. (Reference Bezem, Buchholtz, Grayson and Shulman2021), where the authors state:Footnote
3
Voevodsky chose not to include higher inductive types, nor inductive types, in UniMath for two chief reasons. Firstly, it was (and still is) not clear how to specify precisely what a definition of a higher inductive type consists of […]. Secondly, Voevodsky planned to prove the consistency of UniMath in a series of papers and realised that adding inductive types and higher inductive types to the system would dramatically increase the length of the series and the burden of writing them; as it was, he died before completing the project.
UniMath introduces some specific Unicode notationsFootnote 4 for standard constructions in Type Theory. The most relevant ones for our code are the following.
Let ![]() be a type and
be a type and ![]() a type family. The corresponding dependent pair type is denoted (up to
a type family. The corresponding dependent pair type is denoted (up to
![]() $\alpha$
-conversion) by
$\alpha$
-conversion) by ![]() . Its infix constructor for terms is
. Its infix constructor for terms is ![]() so that we can introduce
so that we can introduce ![]() given suitable terms
given suitable terms ![]() and
and ![]() Projections are denoted by pr1 and pr2 but are usually renamed in a case-by-case basis. Similarly,
Projections are denoted by pr1 and pr2 but are usually renamed in a case-by-case basis. Similarly, ![]() denotes a dependent product type. A dependent function can be introduced by lambda abstraction such as
denotes a dependent product type. A dependent function can be introduced by lambda abstraction such as ![]() where b is a placeholder for a term of B x in which the variable
where b is a placeholder for a term of B x in which the variable ![]() may appear.
may appear.
If ![]() is just a type then the usual product and function types are denoted by
is just a type then the usual product and function types are denoted by ![]() and
and ![]() , respectively. Internally, they are encoded as special cases of Sigma and Pi types in which the type family is the constant function of value B.
, respectively. Internally, they are encoded as special cases of Sigma and Pi types in which the type family is the constant function of value B.
The type of equivalences between two types A and B is denoted by ![]() Its terms consist of a function in
Its terms consist of a function in ![]() and a proof that it has contractible fibres.
and a proof that it has contractible fibres.
Given a natural ![]() the standard finite set of size n is defined as
the standard finite set of size n is defined as ![]() This type, together with a proof that it is indeed a set, can be retrieved with stnset
This type, together with a proof that it is indeed a set, can be retrieved with stnset ![]() . When
. When ![]() is smaller then n, whenever i and n are numerals, we can promptly get the corresponding term with the notation
is smaller then n, whenever i and n are numerals, we can promptly get the corresponding term with the notation ![]() .
.
2.1 Preliminary definitions
In order to support the formalisation of universal algebra, we have enriched UniMath’s standard library with many new concepts and notations. These are introduced in Vectors.v, Lists.v, MoreLists.v, SortedTypes.v and HVectors.v files.
The file Vectors.v contains our implementation of the datatype vec for homogeneous vectors of fixed length. We changed the implementation of list in Lists.v in two aspects. First of all, we redefined lists in terms of the new datatype vec instead of using the ad hoc type iterprod in the standard version of the file. Moreover, we changed a couple of theorems from opaque (![]() conclusion) to transparent (
conclusion) to transparent (![]() conclusion). The latter changes are needed to make terms compute correctly. The file MoreLists.v contains notations for lists, such as
conclusion). The latter changes are needed to make terms compute correctly. The file MoreLists.v contains notations for lists, such as ![]() for list literals and
for list literals and ![]() for cons, together with additional properties which cannot be found in the standard library.
for cons, together with additional properties which cannot be found in the standard library.
The type hvec in HVectors.v denotes heterogeneous vectors:Footnote
5
if v is a vector of types U1, U2,…, Un, then hvec v is the product type ![]() . We introduce several basic operations on heterogeneous vectors. Often they have the same syntax as the corresponding operations on plain vectors and a name which begins with the prefix h. We also introduce notations for heterogeneous vectors, such as
. We introduce several basic operations on heterogeneous vectors. Often they have the same syntax as the corresponding operations on plain vectors and a name which begins with the prefix h. We also introduce notations for heterogeneous vectors, such as ![]() for a literal and
for a literal and ![]() for prefixing.
for prefixing.
Sorted types are types indexed by elements of another type (the index type), so that an element of sUU S is an S-sorted type, that is an S-indexed family of types. For functions, ![]() denotes the type of S-sorted mapping between X and Y, that is of S-indexed families of functions
denotes the type of S-sorted mapping between X and Y, that is of S-indexed families of functions ![]() .
.
More prominently, for any S-sorted type X, its lifting to list S is denoted by X * and is ruled by the identity ![]() . Accordingly, if f is an indexed mapping between S-indexed types X and Y, then f ⋆⋆ is the lifting of f to a list S-indexed mapping between
. Accordingly, if f is an indexed mapping between S-indexed types X and Y, then f ⋆⋆ is the lifting of f to a list S-indexed mapping between ![]() and
and ![]() . This operation
. This operation ![]() is indeed functorial, and we prove that in a form which does not require function extensionality, since resorting to axioms would break computability of terms.
is indeed functorial, and we prove that in a form which does not require function extensionality, since resorting to axioms would break computability of terms.
2.2 Signatures and algebras
We start by defining a multi-sorted signature to be made of a decidable set of sorts along with operations classified by arities and result sorts, as in standard practice.
Given ![]() we introduce the projection sorts
we introduce the projection sorts ![]() to denote the set of its sorts and names
to denote the set of its sorts and names ![]() to denote its set of operations names. If
to denote its set of operations names. If ![]() is also given, then ar
is also given, then ar ![]() represent its arguments and output sorts. These can also be accessed separately with sort
represent its arguments and output sorts. These can also be accessed separately with sort ![]() and arity
and arity ![]() .
.
Note that, in a signature, the set of sorts should be a decSet: this is a type whose equality is decidable, as defined in the file DecSet.v. We need this extra property because – as we previously stated – we want to evaluate terms in the UniMath engine: we can achieve that by pushing sorts into a stack, and we need to check that the very stack contains certain sequences of sorts before applying an operator symbol. Note also that a decSet enjoys the defining property of an hSet. Operators are only required to be in hSet.
A signature may be alternatively specified through the type signature_simple. In a simple signature, the types for sorts and operation symbols are standard finite sets and the map from operation symbols to domain and range is replaced by a list. In this way, the definition of a new signature is made simpler.

Single-sorted signatures are then defined as special cases of signature_simple.

Moving to the file Algebras.v, we define an algebra over a given signature
![]() $\sigma$
to be, as usual, support types indexed by sorts together with operations with appropriate sorts:
$\sigma$
to be, as usual, support types indexed by sorts together with operations with appropriate sorts:

Given an algebra ![]() we can access its underlying types with support
we can access its underlying types with support ![]() and its operations with ops A. If the name nm of such an operation is given, then we can access the domain and range of the corresponding operation as interpreted in A with dom
and its operations with ops A. If the name nm of such an operation is given, then we can access the domain and range of the corresponding operation as interpreted in A with dom ![]() and rng
and rng ![]() respectively.
respectively.
We declare the projection support as a type coercion. Moreover, as for signatures, we simplify the building term for algebras when starting from a simple signature:

A similar proof-term (make_algebra_simple_single_sorted) is given for single-sorted signatures.
All of these notions allow us to define algebra homomorphisms:

The notation ![]() is also introduced as an alternative form for “hom A1 A2”. A special case is when the support of the target algebra A2 is comprised of sets, that is when we have an inhabitant of
is also introduced as an alternative form for “hom A1 A2”. A special case is when the support of the target algebra A2 is comprised of sets, that is when we have an inhabitant of

In this case, ishom is a property and ![]() is a set:
is a set:

Next, we prove – by lemmas ishomid and ishomcomp – that the identity function determines an identity homomorphism and that the property ishom is closed under composition.
2.3 Terms and free algebras
The file Algebras.v is closed by the construction of the unit algebra and a proof of its finality among those defined over its signature:

However, we are mostly interested in the initial object of the category of algebras, namely the algebra of terms over a given signature. In standard textbooks, the set of terms over a signature
![]() $\sigma$
and a (disjoint) set
$\sigma$
and a (disjoint) set
![]() $V$
of variables is defined as the least set including
$V$
of variables is defined as the least set including
![]() $V$
and closed under application of symbols of
$V$
and closed under application of symbols of
![]() $\sigma$
.
$\sigma$
.
Without recurring to general inductive types, in Terms.v we implement this notion using an alternative device, based on reverse Polish notation and value stacks.
In our formalisation, we start with the special case where the set of variables
![]() $V$
is empty. The rough and general idea can be sketched as follows:
$V$
is empty. The rough and general idea can be sketched as follows:
-
1. A sequence of function symbols is thought of as a series of commands to be executed by a stack machine whose stack is made of sorts, and which we define by means of a maybe monad we construct from raw in Maybe.v.

-
2. When an operation symbol is executed, its arity is popped out from the stack and replaced by its range. When a stack underflow occurs, or when the sorts present in the stack are not the ones expected by the operator, the stack goes into an error condition which is propagated by successive operations. We implement this process by means of two functions:

The former is the stack transformation corresponding to the execution of the operation symbol nm. The latter returns the stack corresponding to the execution of the entire oplist argument starting from the empty stack. The list is executed from the last to the first operation symbol. Several additional lemmas are required in order to make us able to handle stacks – by concatenating, splitting, etc. – without incurring failures breaking down the whole process.Footnote 6
-
3. Finally, we define a term to be just a list of operation symbols that, after being executed by oplistexec, returns a list of length one with appropriate sort:Footnote 7

The implementation of build_term is quite straightforward. It concatenates nm and the oplists underlying the terms in v and builds a proof that the resulting oplist is a term from the proofs that the elements of v are terms. The princop and subterms accessors are projections of a more complex operation called term_decompose which breaks a term in principal operation symbols nm and subterms v, and, at the same time, provides the proof-terms that characterise their behaviour.
2.4 Induction on terms
At this point, we proceed in proving induction over terms. The inductive hypothesis, being quite complex, is stated in the term_ind_HP type.

Given a family P of types, indexed by a sort s and a term over s, the inductive hypothesis is a function that, given an operation symbol nm, a sequence of terms v, and a sequence of proofs of P for all terms in v, is able to build a proof of P for the term build_term nm v, that is
![]() $nm(v_1, \ldots, v_n)$
. The identifier h1map_vec simply denotes a variant of vec_map for heterogeneous vectors. Given this auxiliary definition, the induction principle for terms may be easily stated as follows:
$nm(v_1, \ldots, v_n)$
. The identifier h1map_vec simply denotes a variant of vec_map for heterogeneous vectors. Given this auxiliary definition, the induction principle for terms may be easily stated as follows:

The proof proceeds by induction on the length of the oplist underlying t, using the term_ind_onlength auxiliary function.
Simple examples of use of the induction principle on terms are the depth and fromterm functions. The former computes the depth of a term, and the latter is essentially the evaluation map for ground terms in an algebra. The h2lower proof term that appears in the definition of fromterm is just a technicality needed to convert between types that are provably equal but not convertible. This might be replaced by a transport, if we were not interested in computability. The same can be said for the proof term h1lift, later in the definition of term_ind_step.

In order to reason effectively on inductive definitions, we need an induction unfolding property. For natural numbers, it is
which means that the result of applying the recursive definition to S n may be obtained by applying the recursive definition to n and then the inductive hypothesis. While this induction unfolding properties are provable just by ![]() for many inductive types, this does not hold for terms, and a quite complex proof is needed:
for many inductive types, this does not hold for terms, and a quite complex proof is needed:

Notice that many of the definitions which appear in Terms.v are declared as ![]() . This is so because they are considered internal implementation details and should not be used unless explicitly needed. In particular, this holds for a set of identifiers that will be redefined in VTerms.v to work on terms with variables. Since sometimes it may be convenient to have specialised functions that only work with ground terms, they are exported through a series of notations, such as
. This is so because they are considered internal implementation details and should not be used unless explicitly needed. In particular, this holds for a set of identifiers that will be redefined in VTerms.v to work on terms with variables. Since sometimes it may be convenient to have specialised functions that only work with ground terms, they are exported through a series of notations, such as

2.5 Terms with variables and free algebras
Considering terms with variables is what we do in file VTerms.v. The idea is that a term with variables in
![]() $V$
over a signature
$V$
over a signature
![]() $\sigma$
is a ground term in a new signature where constant symbols are enlarged with the variables in
$\sigma$
is a ground term in a new signature where constant symbols are enlarged with the variables in
![]() $V$
. Variables and corresponding sorts are declared in a varspec (variable specification), while vsignature builds the new signature.
$V$
. Variables and corresponding sorts are declared in a varspec (variable specification), while vsignature builds the new signature.

The proof-terms namelift and varname are the injections of, respectively, operation sysmbols and variables in the extended signature. Then, a list of definitions comes: they essentially introduce terms with variables by resorting to ground terms.

Finally, in FreeAlgebras.v, we pack terms and the build_term operation into the algebra
![]() $T_\sigma (V)$
of terms over a given signature
$T_\sigma (V)$
of terms over a given signature
![]() $\sigma$
and set of variables
$\sigma$
and set of variables
![]() $V$
. For this algebra, we prove the expected universal property:
$V$
. For this algebra, we prove the expected universal property:

In TermAlgebras.v, we just consider the special case of FreeAlgebras.v for the empty set of variables, that is for ground terms. In this case, the universal mapping property is replaced by the initiality of the ground term algebra.
2.6 Relation to W-types
W-types are a family of inductive types first introduced in Martin-Löf (Reference Martin-Löf1984) as a way to encapsulate the concept of constructive well ordering and transfinite induction. They can be also used to express strictly positive inductive types, as proven in Abbott et al. (Reference Abbott, Altenkirch, Ghani, Díaz, Karhumäki, Lepistö and Sannella2004). The work of Hugunin (Reference Hugunin, de’, Berardi and Altenkirch2021) shows that interesting computational properties can be retained when doing so. When introduced on top of a given intuitionistic type theory, they provide then a robust foundation for reasoning about inductive data types and recursion within the framework of constructive mathematics.Footnote 8
To interpret their defining rules, one can think of a W-type as a type of rooted, well-founded trees with certain constraints for branching. The formation rule
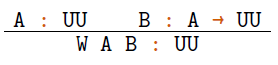
requires a type A for the label of the nodes and a type family ![]() for specifying arities. A node labelled with
for specifying arities. A node labelled with ![]() can be thought of as having
can be thought of as having ![]() children. Accordingly, in order to introduce a new canonical term, one needs to specify a label
children. Accordingly, in order to introduce a new canonical term, one needs to specify a label ![]() for the root node and a subtree for any term of type
for the root node and a subtree for any term of type ![]() by means of a function
by means of a function ![]() . This is stated in the introduction rule.
. This is stated in the introduction rule.

The elimination rule
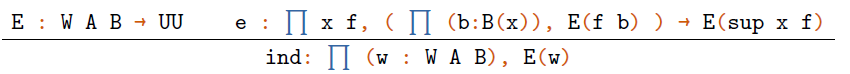
tells us how to inhabit the predicate ![]() for all terms of type W A B. Given
for all terms of type W A B. Given ![]() and
and ![]() , it requires us to produce a proof
, it requires us to produce a proof ![]() , that is: to prove that the predicate holds for the canonical term specified by x and f; in doing so, one has to assume that E holds for any of the relevant subtrees (i.e.,
, that is: to prove that the predicate holds for the canonical term specified by x and f; in doing so, one has to assume that E holds for any of the relevant subtrees (i.e., ![]() ).
).
Finally, the computation rule states that the proof ind just obtained is judgementally the same as the one obtained by applying e to the proof term for subtrees obtained by ind.
This definition of W-types is not available in UniMath. Nevertheless, it is possible to reason internally about types which behave like W-types by means of homotopy W-types, which are presented in details by Awodey et al. (Reference Awodey, Gambino and Sojakova2012).
Given ![]() and
and ![]() , a corresponding homotopy W-type consists of a type together with functions encapsulating the introduction and elimination principle and satisfying the appropriate computation rule w.r.t. the equality type. This can be expressed in UniMath as follows.
, a corresponding homotopy W-type consists of a type together with functions encapsulating the introduction and elimination principle and satisfying the appropriate computation rule w.r.t. the equality type. This can be expressed in UniMath as follows.

A classical approach, as the one employed by Capretta (Reference Capretta, Bertot, Dowek, Hirschowits, Paulin and Théry1999), would be to resort to W-types to define free algebras. Since general inductive definitions are not available in our formal system, we cannot do that while maintaining the computational properties we are interested in. Nonetheless, it is still expected for our structure of a free algebra to resemble that of a W-type. We show this is indeed the case in WTypes.v for any ground algebra of single-sorted signature
![]() $\sigma$
.Footnote
9
$\sigma$
.Footnote
9
Our main goal is to identify a type ![]() and a type family
and a type family ![]() with the aim of constructing a homotopy W-type
with the aim of constructing a homotopy W-type
whose first component is judgmentally the carrier type of the ground algebra with signature
![]() $\sigma$
. So U
$\sigma$
. So U ![]() .
.
The idea is to identify any ground term ![]() with an inductively defined tree of ground terms. The root is t itself and, if a node is a term
with an inductively defined tree of ground terms. The root is t itself and, if a node is a term ![]() , its children are the components of subterms t
′. We can label each node of this tree with its principal operation which has type A
, its children are the components of subterms t
′. We can label each node of this tree with its principal operation which has type A ![]() . The number of children of a node labelled by
. The number of children of a node labelled by ![]() is then the arity of the label, precisely B(a)
is then the arity of the label, precisely B(a) ![]() This reasoning motivates our choices of A and B and can be expanded to identify crucial terms to derive the definitions of sup, ind and beta.
This reasoning motivates our choices of A and B and can be expanded to identify crucial terms to derive the definitions of sup, ind and beta.
As a matter of fact, we have already introduced a method to obtain a term from an operation and an appropriate listing of subterms, namely
This does the same job of the introduction term
we are trying to define, but their types are not convertible. Still, by definition of A and since
![]() $\sigma$
is single sorted we have that the build_gterm’s type is convertible to
$\sigma$
is single sorted we have that the build_gterm’s type is convertible to ![]() . Moreover we prove equivalences
. Moreover we prove equivalences

The application of the latter to build_gterm is our definition of sup.
In a similar manner, the elimination term
is the application to
of an appropriate equivalence ind_weq. We leave out its full construction, but we mention the following lemmas.

Here, and whenever we do not explicitly bound it as a variable, f is just notation for gtweq_sec nm v, that is the image of v under the first equivalence introduced above. ind_HP stands for the type of e_s in the definition of homotopy W-type. More precisely,
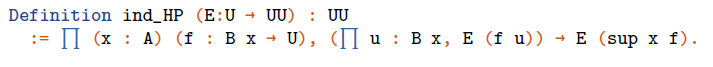
Finally, we discuss the proof of the computation path
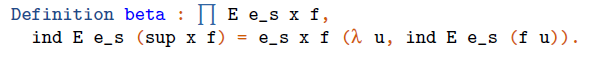
Here the parameters E, e_s and f each have a type involved in a previously proved equivalence. We first consider the corresponding result quantified over the domains of these equivalences. To be clear, instead of quantifying over ![]() we do it over
we do it over ![]() and we write gtweq_sec nm v in place of f. We do the same for E and e_s. After inhabiting the new type, we can prove our goal beta by the well-known lemma of UniMath weqonsecbase. This approach allows us to manage many technical complications depending on the fact that equivalences are not judgementally invertible.
and we write gtweq_sec nm v in place of f. We do the same for E and e_s. After inhabiting the new type, we can prove our goal beta by the well-known lemma of UniMath weqonsecbase. This approach allows us to manage many technical complications depending on the fact that equivalences are not judgementally invertible.
Now, coming to the actual proof, we want to make use of

which, once again, is the intended path in the wrong types. To conclude the proof, it suffices to find an equivalence which maps (propositionally) both sides of term_ind_step to the corresponding sides of beta. This is a delicate step since the equivalence we choose here is proof relevant: its proof term must be manageable, and it must interact nicely with many of the other constructions presented until now. We opt for
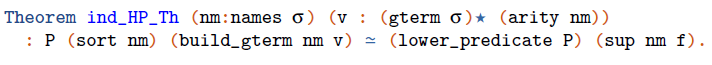
which is actually a lemma we already used to construct HP_weq.
Proving that this equivalence respects the right-hand sides of term_ind_step, and beta is not trivial. In particular, the proof of theorem ind_HP_Hypo_h2map revealed a rather challenging task because of several technicalities in relating our heterogeneous vectors to dependent functions.Footnote 10
2.7 Equations and equational algebras
Equations and their associated structures are key notions in universal algebra. Although an extensive treatment of equational algebras and varieties is out of the scope of the present work, the basic definitions are already present in our implementation in the file EqAlgebras.v.
In our setting, an equation is a pair of terms (with variables) of the same sort. Their intended meaning is to specify identities law where variables are implicitly universally quantified.

The associated projections are denoted eqsort, lhs and rhs , respectively. An equation system is just a family of equations.

Then, we pack all the above data into an equational specification that is a signature endowed with an equation system (and the necessary variable specification).
The interpretation of an equation is easily defined using the holds that checks if the universal closure of an equation e holds in an algebra is given as follows:

From this, it is immediate to define the type eqalgebra of equational algebras as those algebras in which all the equations of a given equational specification hold.
2.8 Categorical structures
Universal algebra has a natural and fruitful interplay with category theory, as discussed by, e.g., Hyland and Power (Reference Hyland and Power2007). As claimed in the introduction, our mechanisation includes basic categorical constructions for organising and reasoning about universal algebra structures. In agreement with the general philosophy of univalent mathematics,Footnote 11 we can prove that the categories we are interested in – of algebras and equational algebras – are univalent indeed.
In order to develop formal proofs of that property, two possible strategies are available. A simplest one consists of building the desired category from scratch and then prove that univalence holds between any pair of isomorphic objects. However, experience has shown that this strategy often lacks a certain naturalness, and it makes the steps involved in the construction hard. The second available strategy has revealed practicable in a more efficient way: we define the desired category in a step-by-step construction by adding layers to a base category already given. Such a notion of layer corresponds precisely to a displayed category as formulated by Ahrens and Lumsdaine (Reference Ahrens and Lumsdaine2019). Displayed categories can be thought of as the type-theoretic counterpart of fibrations and constitute a widely adopted instrument to reason about categories even at higher dimensions in the UniMath library.Footnote 12
To this end, a simple approach would be to proceed in two separate steps, first build the desired categories, then write the proofs that they are univalent. After defining a displayed category over a base category, we can then build a total category whose univalence is proven by checking univalence for the base category and a displayed version of univalence for the category displayed over the base. This is a generalised version of the so-called structure identity principle, introduced first by Aczel (Reference Aczel, Buss, Kohlenbach and Rathjen2011) as invariance of all structural properties of isomorphic structures (broadly considered).
Since the type of morphisms in UniMath’s categories are sets, we need to restrict our attention to algebras whose carrier is not just an index type but an indexed hSet (denoted as shSet in the library). The special case of algebras whose support is an shSet is the hSetAlgebra type.
To build our category of algebras, we apply that very principle: the structure of algebras and homomorphisms is displayed over a base category of sorted hSets, as proven in our lemma.
In a bit more detailed manner, when building the main category of algebras over a given signature
![]() $\sigma$
,
$\sigma$
,
-
• We associate to each sorted-hSet its family of algebras;
-
• To each sorted-function, we associate the property ishom;
-
• We then use the fact that the identity sorted-function defines an algebra homomorphism, and that ishom is closed under composition of sorted-functions, as stated by ishomid and ishomcomp, respectively;Footnote 13
-
• Finally, we use the UniMath lemma is_univalent_disp_from_SIP_data to prove displayed univalence by showing that the property of being an algebra is an hSet indeed, and that any two interpretations of symbols of
 $\sigma$
are equal whenever the identity sorted-function is an homomorphism w.r.t. these given assignments.
$\sigma$
are equal whenever the identity sorted-function is an homomorphism w.r.t. these given assignments.
At this point, proving that the base category of shSets is univalent turned out to be non-trivial. Nevertheless, we managed the issue by tweaking the proof terms already constructed for functor categories in UniMath. The resulting total category of algebras is therefore univalent in the usual sense.
Turning now to equational algebras, we do not have to start the construction again from scratch: within the displayed category formalism we can identify the ‘substructure’ of algebras over shSets satisfying a system of equations. In other terms, we can is_eqalgebra .
Again, proving displayed univalence for this layer is not difficult, so that the total category of equational algebras over a system of equations is univalent, as required.
Finally, we rephrase the universal property of the term algebra shown in Section 2.3: we can state its initiality in the category of algebras over a given
![]() $\sigma$
by means of the proof-term made of the of the algebra itself and the contractibility of out-going homomorphisms, previously constructed.
$\sigma$
by means of the proof-term made of the of the algebra itself and the contractibility of out-going homomorphisms, previously constructed.
The reader interested in the details of these categorical results is referred to our code located in the subdirectory Universal_Algebra .
3. Three applications
In this section, we want to illustrate by simple examples how to use our framework in three different settings.
3.1 List algebras
We start with a very simple multi-sorted example. We will show how to specify a signature in our framework and how to interpret a list datatype as an algebra.Footnote 14
We will need two sorts, one for elements and the other for lists. Correspondingly, we name the two elements •0 and •1 of the standard finite set with two elements ![]() .
.

Our signature for the language of lists will consist of two operation symbols for the usual constructors nil and cons, respectively.
Such a signature is encoded with a list of pairs. Each pair describes the input (a list of sorts) and the output (a sort) for the corresponding constructor.

For enhanced readability, we assign explicit names to the operator symbols.

Now, we can endow the list datatype with the structure of an algebra over list_signature by using the list constructors nil and cons .
We fix a type A for our elements. Then, the class of algebras over list_signature is given byFootnote 15

From now on in this section, lemmas are just simple verification of convertibility. They are all proven by reflexivity and the proof scripts are omitted.
To begin with, we check that the sort of elements is
![]() $A$
and the sort of lists is given by the associated list datatype:
$A$
and the sort of lists is given by the associated list datatype:

Next, we inspect the associated algebra operations. We can extract and currify them with ops’ . First, let us consider the empty list constructor.
As expected, it reduces to the usual nil constructor.
For the list cons constructor, the situation is more complicated. The domain of the constructor is the product ![]() meaning that the constructor has two (uncurried) arguments
meaning that the constructor has two (uncurried) arguments
Still, it reduces to the usual list cons.

3.2 Equational algebras of monoids
From now on, we will consider single sorted examples for the sake of simplicity.
In this Section, we will discuss the eqalgebra of monoids.Footnote 16
To define single sorted signatures, our function make_signature_simple_single_sorted is a handy shorthand – introduced in Section 2.2 – taking only a list of natural numbers.
Monoids are already defined in UniMath: given M a monoid , unel M accesses its identity, and op accesses its operation.
Similarly to what we did in the previous section with lists, we endow monoids with the structure of a monoid algebra.

Next, we provide a variable specification, that is an hSet of variables together with a map from variables to sorts. Since monoid_signature is single-sorted, the only available sort is tt.
Then, we build the associated algebra of open termsFootnote 17 that will be used to specify the equations of the theory of monoids.

Term variables are associated to natural numbers. In this case, three variables x, y, z will suffice for our needs:

Now, we have all the ingredients to specify our equations: the monoid axioms of associativity, left identity and right identity (where == is just a shorthand for giving terms of the relevant type equation monoid_signature monoid_varspec).

We pack the above equations together into an equation system (monoid_axioms ) and its associated equational specification (monoid_eqspec ); finally, we define the class of equational algebras of monoids monoid_eqalgebra .Footnote 18
Next, we want to show that every ‘classical’ monoid
![]() $M$
has a natural structure of equational algebra.
$M$
has a natural structure of equational algebra.
We have two show that
![]() $M$
is a model for our equation system. Let us consider the left-identity axiom
$M$
is a model for our equation system. Let us consider the left-identity axiom

As you see, we fix the variable evaluation
![]() $\alpha$
, then we observe that our goal reduces to the same law expressed in the usual language of monoids – op for the product, unel M for the identity,
$\alpha$
, then we observe that our goal reduces to the same law expressed in the usual language of monoids – op for the product, unel M for the identity,
![]() $\alpha$
$\alpha$
![]() for the first variable x – and then the goal is solved at once by applying the corresponding monoid axiom lunax
.
for the first variable x – and then the goal is solved at once by applying the corresponding monoid axiom lunax
.
The other two laws – for right identity and associativity – are proven in the same way.
Thus, we can now pack everything into a monoid eqalgebra with is_eqalgebra_monoid and make_monoid_eqalgebra .
3.3 Algebra of booleans and Tarski’s semantics
We conclude the code survey with a further example based on a simple single sorted algebraic language: the algebra of booleans and its connectives.Footnote 19
The language considered has the usual boolean operators: truth, falsity, negation, conjunction, disjunction and implication. Arities can be simply specified by naturals (the number of arguments).
We use the function make_signature_simple_single_sorted to build a signature from the list of arities:
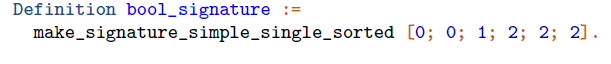
Obviously, the type of booleans is already defined in UniMath, together with its usual constants and operations: false , true , negb , andb , orb , implb .
Now, booleans form an hSet, which is denoted boolset . It is easy to organise all of those constituents into an algebra for our signature by specifying the translation:

Next, we build the algebra of (open) terms, that is, boolean formulas.
This is done in two steps. First, we give a variable specification, that is a set of type variables:
Then, we define the algebra of terms and the associated constructors.

Finally, we use the universal property of the term algebra to define the interpretation of boolean formulas:

At this point, we can check the effectiveness of our definitions with some applications.
To set-up our tests, we introduce three variables x, y, z
and a simple evaluation function v for variables that assigns ![]() to the variable x and y (the variable of index
to the variable x and y (the variable of index
![]() $0$
and
$0$
and
![]() $1$
) and
$1$
) and ![]() otherwise. Now, we can interpret formulas such as
otherwise. Now, we can interpret formulas such as
![]() $x \wedge (z \to \neg y)$
:
$x \wedge (z \to \neg y)$
:

The reader is invited to notice that the choice of the lazy strategy is not accidental. Computations required to evaluate such a proof term are pretty heavy and the standard call by value strategy does not seem able to produce a result in reasonable time.
A few other examples are available in our code as, for instance, a proof of Dummett’s tautology:

Notice that this formal proof is just a case analysis for truth-tables in disguise: we instantiate the values of x and y by applying ![]() twice, but the remaining job is left to the computing mechanism of Coq, which is able to autonomously verify that the evaluation does yield the value
twice, but the remaining job is left to the computing mechanism of Coq, which is able to autonomously verify that the evaluation does yield the value ![]() in all cases – we only need to apply idpath.
in all cases – we only need to apply idpath.
Conclusions
We have surveyed our UniMath library for universal algebra, covering the fundamental concepts of multi-sorted signatures, algebras and equational algebras.
We have shown how to implement term algebras over a signature without relying on general inductive constructions (as prescribed by the UniMath formal language) and proven that our single sorted ground term algebras have the structure of homotopy W-types.
Additionally, we showed that algebras (and algebras modulo equations) over a given signature define a univalent category, whenever their carriers are (sorted) hSets.
Finally, we have instantiated with three concrete examples of algebraic structures our general framework for formalising universal algebra in UniMath.
Future work
We plan to enhance our implementation along three directions:
-
1. First of all, we wish to streamline the interface provided by the library. With the current state of implementation, the user is exposed to many technical details, which have no theoretical relevance. These include the internal signatures generated by vsignature for dealing with variables in terms and the existence of two term algebras, one for ground terms, the other for general terms, while the former should only be a particular case of the latter. We plan to redesign the interface in order to hide the internal details as much as possible. Furthermore, the interface for heterogeneous vectors might be generalised to make the HVectors.v module more useful outside of the scope of our library.
-
2. Next, we intend to push further the mathematical salience of the library. This means, for instance, generalising the result relating ground term algebras and W-types to the multi-sorted case. Since we expect to require indexed homotopy W-types to keep track of the sorts, we aim at providing UniMath with a detailed formalisation of that notion, following the analysis given by Sattler (Reference Sattler2015). Moreover, we plan to complete the treatment of equational algebras by defining the initial algebra of terms modulo equational congruence. Additionally, we expect to give formal proofs of some known central results in universal algebra, starting from the homomorphism theorems and Birkhoff’s variety theorem.
-
3. Finally, to extend the library with refined applications and examples of univalent reasoning. This would give evidence that even the minimalist environment of UniMath does allow its user to approach mechanised mathematics with the advantages of both univalent reasoning – to handle equivalent objects as naturally as in informal mathematics – and the automation process of the proof assistant – to be smartly used for performing “internal” implementations in order to leave all computations with no demonstrative significance to the machine. Among future formalisations to integrate in our library for univalent universal algebra, we are considering algebraic models for computations, including lambda-algebras for
 $\lambda$
-calculi and their modal extensions.Footnote
20
$\lambda$
-calculi and their modal extensions.Footnote
20
Related work
Ours is not the first mechanisation of universal algebra currently available in the literature.
A classical work on formalising this area of mathematics in dependent type theory is Capretta (Reference Capretta, Bertot, Dowek, Hirschowits, Paulin and Théry1999), where he systematically uses setoids in Coq to handle equality on structures. Another attempt, still based on setoids, has been carried out in Agda by Gunther et al. (Reference Gunther, Gadea and Pagano2018).
The works of DeMeo (Reference DeMeo2021a,b); DeMeo and Carette (Reference DeMeo and Carette2021) draw on the multi-sorted version of Abel (Reference Abel2021) to develop an extensive and setoid-based Agda library on single-sorted universal algebra that strives to be as powerful as Abel’s formalisation but a bit more sensitive to foundational aspects.
Very recently, the paper Reynolds and Monahan (Reference Reynolds and Monahan2024) presents a formalisation in Coq of the theory of institutions based on the approach to universal algebra by Gunther et al. (Reference Gunther, Gadea and Pagano2018).
On the categorical side, initial semantics furnishes elegant techniques for studying induction and recursion principles within a general algebraic setting with applications in programming languages and logic. Assuming univalence, steady research activity has produced over the time a number of contributions to the UniMath library, see e.g. Ahrens et al., (Reference Ahrens, Hirschowitz, Lafont, Maggesi, Ghica and Jung2018, Reference Ahrens, Hirschowitz, Lafont, Maggesi and Geuvers2019b,c, Reference Ahrens, Matthes and Mörtberg2022).
From a HOTT-UF perspective, the formalisation of universal algebra by Lynge (Reference Lynge2017) – further developed in Lynge and Spitters (Reference Lynge and Spitters2019) – outline a framework that more closely compares with ours, since it is still based on univalent reasoning, though implemented in the Coq-HoTT (Bauer et al., Reference Bauer, Gross, Lumsdaine, Shulman, Sozeau, Spitters, Bertot and Vafeiadis2017) extension for the Calculus of the (Co)Inductive Constructions.
Acknowledgements
We thank the anonymous referee for valuable comments and suggestions. This work was partially supported by: the MIUR project PRIN 2017FTXR7S IT-MATTERS (Methods and Tools for Trustworthy Smart Systems); the MIUR project PRIN 2017JZ2SW5 ‘Real and Complex Manifolds: Topology, Geometry and holomorphic dynamics’ the project SERICS ‘Security and Rights in CyberSpace’ – PE0000014, financed within PNRR, M4C2 I. 1. 3, funded by the European Union - NextGenerationEU; the PNRR project FAIR – Future AI Research (PE00000013), Spoke 9 - Green-aware AI, under the NRRP MUR program funded by the NextGenerationEU; Istituto Nazionale di Alta Matematica – INdAM groups GNAMPA, GNCS and GNSAGA.
Competing interests
The authors have no relevant financial or non-financial interests to disclose.






