No CrossRef data available.
Article contents
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
Part of:
Multiplicative number theory
Algebraic number theory: global fields
Sequences and sets
Polynomials and matrices
General field theory
Published online by Cambridge University Press: 14 August 2019
Abstract
We prove that for every sufficiently large integer 
$n$, the polynomial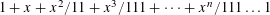 
$1+x+x^{2}/11+x^{3}/111+\cdots +x^{n}/111\ldots 1$ is irreducible over the rationals, where the coefficient of 
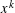$x^{k}$ for 
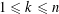$1\leqslant k\leqslant n$ is the reciprocal of the decimal number consisting of 
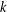$k$ digits which are each 
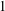$1$. Similar results following from the same techniques are discussed.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
References
Apostol, T. M., Resultants of cyclotomic polynomials. Proc. Amer. Math. Soc.
24
1970, 462.10.1090/S0002-9939-1970-0251010-XGoogle Scholar
Dickson, L. E., History of the Theory of Numbers, Vol. I: Divisibility and Primality, Chelsea (New York, 1966).Google Scholar
Dresden, G., Resultants of cyclotomic polynomials. Rocky Mountain J. Math.
42
2012, 1461–1469.10.1216/RMJ-2012-42-5-1461Google Scholar
Dumas, G., Sur quelques cas d’irréductibilité des polynômes à coefficients rationnels. J. Math. Pures Appl. (9)
2
1906, 191–258.Google Scholar
Filaseta, M., Coverings of the integers associated with an irreducibility theorem of A. Schinzel. In Number Theory for the Millennium, II (Urbana, IL, 2000), A. K. Peters (Natick, MA, 2002), 1–24.Google Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods, Dover (Mineola, NY, 2011). Originally published by Academic Press (London Mathematical Society Monographs
4 (1974)).Google Scholar
Stewart, C. L., On divisors of Lucas and Lehmer numbers. Acta Math.
211
2013, 291–314.10.1007/s11511-013-0105-yGoogle Scholar