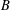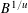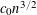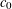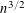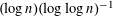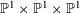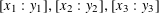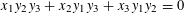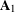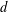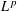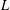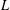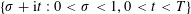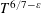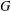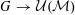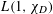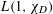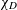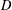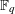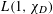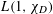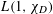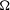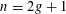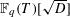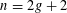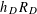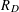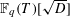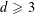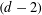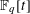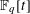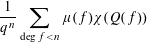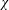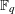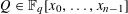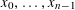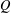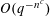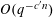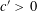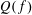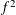Research Article
SARNAK’S SATURATION PROBLEM FOR COMPLETE INTERSECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2018, pp. 1-56
-
- Article
- Export citation
ON A TWISTED VERSION OF LINNIK AND SELBERG’S CONJECTURE ON SUMS OF KLOOSTERMAN SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 437-474
-
- Article
- Export citation
TILING WITH PUNCTURED INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 181-189
-
- Article
- Export citation
THE POWER-SAVING MANIN–PEYRE CONJECTURE FOR A SENARY CUBIC
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2019, pp. 789-830
-
- Article
- Export citation
ANALYSIS IN THE MULTI-DIMENSIONAL BALL
- Part of:
-
- Published online by Cambridge University Press:
- 31 October 2018, pp. 190-212
-
- Article
- Export citation
ON ITERATED PRODUCT SETS WITH SHIFTS
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 831-850
-
- Article
- Export citation
GOLDBACH REPRESENTATIONS IN ARITHMETIC PROGRESSIONS AND ZEROS OF DIRICHLET L-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2018, pp. 57-97
-
- Article
- Export citation
CANCELLATIONS BETWEEN KLOOSTERMAN SUMS MODULO A PRIME POWER WITH PRIME ARGUMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 475-487
-
- Article
- Export citation
HADAMARD MATRICES AND 1-FACTORIZATIONS OF COMPLETE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2019, pp. 488-499
-
- Article
- Export citation
ON SIMPLE ZEROS OF THE DEDEKIND ZETA-FUNCTION OF A QUADRATIC NUMBER FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2019, pp. 851-861
-
- Article
- Export citation
COMPLETENESS OF THE LIST OF SPINOR REGULAR TERNARY QUADRATIC FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2018, pp. 213-235
-
- Article
- Export citation
OPERATOR ALGEBRAIC APPROACH TO INVERSE AND STABILITY THEOREMS FOR AMENABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2018, pp. 98-118
-
- Article
- Export citation
A CONVERSE THEOREM WITHOUT ROOT NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 862-873
-
- Article
- Export citation
COMPLEX MOMENTS AND THE DISTRIBUTION OF VALUES OF
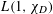 $L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
$L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2018, pp. 236-271
-
- Article
- Export citation
THE ISOPERIMETRIC QUOTIENT OF A CONVEX BODY DECREASES MONOTONICALLY UNDER THE EIKONAL ABRASION MODEL
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2018, pp. 119-129
-
- Article
- Export citation
ELLIPSOIDS ARE THE ONLY LOCAL MAXIMIZERS OF THE VOLUME PRODUCT
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 500-504
-
- Article
-
- You have access
- HTML
- Export citation
THE STEKLOV SPECTRUM OF CUBOIDS
- Part of:
-
- Published online by Cambridge University Press:
- 06 December 2018, pp. 272-310
-
- Article
- Export citation
LINEAR AND QUADRATIC UNIFORMITY OF THE MÖBIUS FUNCTION OVER
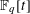 $\mathbb{F}_{q}[t]$
$\mathbb{F}_{q}[t]$
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2019, pp. 505-529
-
- Article
- Export citation
ON THE INTEGRAL FORMULAS OF CROFTON AND HURWITZ RELATIVE TO THE VISUAL ANGLE OF A CONVEX SET
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 874-896
-
- Article
- Export citation
Corrigendum
KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2018, pp. 130-131
-
- Article
-
- You have access
- HTML
- Export citation