No CrossRef data available.
Article contents
A Cauchy criterion for the summability of an infinite integral
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
If a ∈ L(1, T) for every finite T>1, then we say that the infinite integral 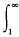 a(u)du is convergent with sum s if
a(u)du is convergent with sum s if 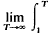 a(u)du = s. It is well known that a necessary and sufficient condition for
a(u)du = s. It is well known that a necessary and sufficient condition for 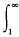 a(u)du to be convergent (with some finite sum s) is that Cauchy's criterion,
a(u)du to be convergent (with some finite sum s) is that Cauchy's criterion,
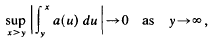
holds. The object of this note is to obtain a similar result for summability (C, α) of 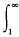 a(u) du which reduces to Cauchy's criterion in the case of convergence. The corresti ponding problem for summable series has been treated by A. F. Andersen in (1).
a(u) du which reduces to Cauchy's criterion in the case of convergence. The corresti ponding problem for summable series has been treated by A. F. Andersen in (1).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1980
References
REFERENCES
(1)Andersen, A. F., A condition for C-summability of negative order, Math. Scand. 7 (1959), 337–346.CrossRefGoogle Scholar
(2)Bosanquet, L. S., Some extensions of M. Riesz's mean value theorem, Indian J. Math. 9 (1967), 65–90.Google Scholar
(3)Hardy, G. H., Theorems connected with Maclaurin's test for the convergence of series, Proc. London Math. Soc. (2) 9 (1911), 126–144.CrossRefGoogle Scholar
(4)Hardy, G. H., Notes on some points in the integral calculus XLVIII: On some properties of integrals of fractional order, Math. Messenger 47 (1918), 145–150.Google Scholar

