Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DeVore, R.
and
Richards, F.
1973.
The degree of approximation by Chebyshevian splines.
Transactions of the American Mathematical Society,
Vol. 181,
Issue. 0,
p.
401.
Scherer, Karl
1974.
Characterization of Generalized Lipschitz Classes by Best Approximation with Splines.
SIAM Journal on Numerical Analysis,
Vol. 11,
Issue. 2,
p.
283.
Scherer, Karl
1975.
Approximation Theory.
p.
189.
Devore, R.
and
Scherer, K.
1976.
Approximation Theory.
Vol. 556,
Issue. ,
p.
167.
Widlund, Olof
1976.
On best error bounds for approximation by piecewise polynomial functions.
Numerische Mathematik,
Vol. 27,
Issue. 3,
p.
327.
Brudnyi, Ju. A.
1976.
Approximation Theory.
Vol. 556,
Issue. ,
p.
73.
Brass, Helmut
1978.
Umkehrsätze beim Trapezvedahren.
Aequationes Mathematicae,
Vol. 18,
Issue. 1-2,
p.
338.
Micula, Gheorghe
and
Micula, Sanda
1999.
Handbook of Splines.
p.
383.
Irodova, I. P.
2015.
Piecewise Polynomial Approximation Methods in the Theory of Nikol’Skiĭ–Besov Spaces.
Journal of Mathematical Sciences,
Vol. 209,
Issue. 3,
p.
319.


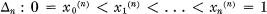 1 be a subdivision of [0, 1], and let
1 be a subdivision of [0, 1], and let 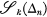 denote the class of functions whose restriction to each sub-interval
denote the class of functions whose restriction to each sub-interval 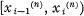 is a polynomial of degree at most
is a polynomial of degree at most 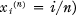
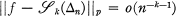
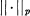 denotes the usual norm in
denotes the usual norm in 